Из различных занимательных задач, связанных с кубом, я упомяну лишь головоломку с вычислением полного сопротивления электрической цепи, образованной ребрами проволочного куба, и тот удивительный факт, что куб может проходить через отверстие в меньшем кубе. В самом деле, стоит вам взять куб так, чтобы одна из его вершин была направлена прямо на вас, а ребра образовали правильный шестиугольник, как вы увидите, что в сечении, перпендикулярном лучу зрения, есть достаточно места для квадратного отверстия, которое чуть больше грани самого куба. В электрической головоломке речь идет о цепи, изображенной на рис. 93.
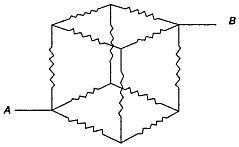
Рис. 93 Электрическая цепь-головоломка.
Сопротивление каждого ребра куба равно одному ому. Чему равно сопротивление всей цепи, если ток течет от Л к В? Инженеры-электрики извели немало бумаги, пытаясь решить эту задачу, хотя при надлежащем подходе найти ее решение совсем несложно.
Все пять Платоновых тел использовались в качестве игральных костей. После куба наибольшую популярность приобрели игральные кости в форме октаэдра. Как сделать такую кость, показано на рис. 94.
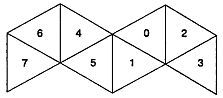
Рис. 94 Как сделать игральную кость в форме октаэдра.
Начертив и вырезав полоску и перенумеровав грани, ее перегибают вдоль ребер, а «открытые» ребра склеивают прозрачной лентой. Получается миниатюрный октаэдр. Сумма очков на противоположных гранях октаэдрической игральной кости, как и обычной кубической, равна семи. При желании с помощью новой кости вы можете показать забавный фокус с отгадыванием задуманного числа. Попросите кого-нибудь загадать любое число от 0 до 7. Положите октаэдр на стол так, чтобы загадавший мог видеть только грани с цифрами 1, 3, 5 и 7, и спросите, не видит ли он задуманного им числа. Если он отвечает утвердительно, вы запоминаете про себя число 1. Затем вы переворачиваете октаэдр так, чтобы загадавшему были видны грани с цифрами 2, 3, 6 и 7, и снова задаете тот же вопрос. На этот раз утвердительный ответ означает, что вы должны запомнить число 2. В третий (и последний раз) вы повторяете свой вопрос, повернув октаэдр так, чтобы загадавший мог видеть грани с цифрами 4, 5, б и 7. Утвердительный ответ в этом случае оценивается числом 4. Сложив оценки всех трех ответов, вы получите задуманное вашим приятелем число. Этот фокус без труда объяснит всякий, кто знаком с двоичной системой счисления. Чтобы легче было отыскать нужные положения октаэдра, как-нибудь пометьте три вершины, которые должны быть обращены к вам, когда вы стоите лицом к зрителю (задумавшему число).
Существуют и другие не менее интересные способы нумерации граней октаэдрической игральной кости. Например, числа от 1 до 8 можно расположить так, что сумма чисел на четырех гранях, сходящихся в общей вершине, будет постоянна. Эта сумма всегда равна 18, однако существует три различных способа нумерации граней (мы не считаем различными кости, которые переходят друг в друга при поворотах и отражениях), удовлетворяющих заданному выше условию.
Изящный способ построения додекаэдра предложил в своей книге «Математический калейдоскоп» Гуго Штейнгауз.[31] Из плотного картона нужно вырезать две фигуры, показанные на рис. 95.
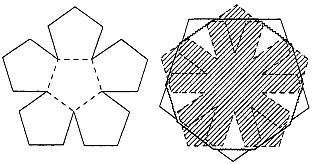
Рис. 95 Вырезав из бумаги две такие фигуры и скрепив их резинкой, вы получите складной додекаэдр.
Стороны пятиугольников должны быть около 2,5–3 см. Лезвием ножа осторожно надрежем картон вдоль сторон внутреннего пятиугольника, с тем чтобы развертка легко сгибалась в одну сторону. Подготовив таким же образом вторую развертку, наложим ее на первую так, чтобы выступы второй развертки пришлись против вырезов первой. Придерживая обе развертки рукой, скрепим их резинкой, пропуская ее попеременно то над выступающим концом одной развертки, то под выступающим концом другой. Ослабив давление руки на развертки, вы увидите, как на ваших глазах, словно по волшебству, возникнет додекаэдр.
Раскрасим модель додекаэдра таким образом, чтобы каждая грань была выкрашена только одним цветом. Чему равно наименьшее число красок, которыми можно раскрасить додекаэдр, если требуется, чтобы любые две смежные грани были разного цвета?
Ответ: наименьшее число красок равно четырем. Нетрудно убедиться, что существуют четыре различных способа наиболее номной раскраски додекаэдра (при этом два раскрашенных додекаэдра будут зеркальными отражениями двух других). Для раскраски тетраэдра также требуется четыре краски, но существует лишь два варианта раскраски, при этом один тетраэдр переходит в другой при зеркальном отражении. Куб можно раскрасить тремя, а октаэдр — двумя красками. Для каждого из этих тел существует лишь один способ наиболее экономной раскраски. Раскрасить икосаэдр можно всего лишь тремя красками, но сделать это можно не менее чем 144 способами. Лишь в шести из них раскрашенные икосаэдры совпадают со своими зеркальными отражениями.
Рассмотрим еще одну задачу. Предположим, что муха, разгуливая по 12 ребрам икосаэдра, проползает по каждому из них по крайней мере один раз. Каков наименьший путь, который должна проделать муха, чтобы побывать на всех ребрах икосаэдра? Возвращаться в исходную точку не обязательно; некоторые ребра мухе придется пройти дважды (из всех пяти Платоновых тел только октаэдр обладает тем свойством, что его ребра можно обойти, побывав на каждом из них лишь по одному разу). Решению задачи может помочь проекция икосаэдра на плоскость (рис. 96).
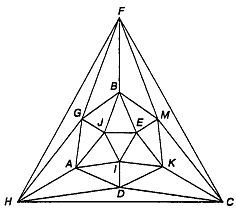
Рис. 96 Проекция икосаэдра на плоскость.
Только следует иметь в виду, что длина всех ребер одинакова.
Поскольку и поныне встречаются чудаки, все еще пытающиеся найти решение задач о трисекции угла и квадратуре круга, хотя давно уже доказано, что ни то, ни другое невозможно, кажется странным, что никто не предпринимает попыток найти новые правильные многогранники сверх уже известных пяти Платоновых тел.
Одна из причин такого парадоксального положения заключается в том, что понять, почему не существует более пяти правильных тел, крайне несложно. Следующее простое доказательство существования не более пяти правильных тел восходит к Евклиду.
Многогранный угол правильного тела должен быть образован по крайней мере тремя гранями. Рассмотрим простейшую из граней: равносторонний треугольник. Многогранный угол можно построить, приложив друг к другу три, четыре или пять таких треугольников. При числе треугольников свыше пяти сумма плоских углов, примыкающих к вершине многогранника, составляет 360° или даже больше, и, следовательно, такие треугольники не могут образовывать многогранный угол. Итак, существует лишь три способа построения правильного выпуклого многогранника с треугольными гранями. Пытаясь построить многогранный угол из квадратных граней, мы убедимся, что это можно сделать лишь из трех граней. Аналогичными рассуждениями нетрудно показать, что в одной вершине правильного многоугольника могут сходиться три и только три пятиугольные грани. Грани не могут иметь форму многоугольников с числом сторон больше пяти, так как, приложив, например, друг к другу три шестиугольника, мы получим в сумме угол в 360°.
Приведенное только что рассуждение не доказывает возможности построения пяти правильных тел, оно лишь объясняет, почему таких тел не может быть больше пяти. Более тонкие рассуждения заставляют прийти к выводу, что в четырехмерном пространстве имеется лишь шесть правильных политопов (так называются аналоги трехмерных правильных тел). Любопытно отметить, что в пространстве любого числа измерений, большем 4-х, существует лишь три правильных политопа: аналоги тетраэдра, куба и октаэдра.
31
Эта игрушка была приложена лишь к первому изданию книги Г. Штейнгауза, в дальнейших изданиях, в том числе и в русском (М.: Гостехиздат, 1949), ее нет.