6. Из двенадцати спичек можно построить прямоугольный треугольник со сторонами в три, четыре и пять единиц, как показано на рис. 59 слева.

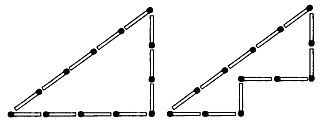
Рис. 59

Его площадь равна шести квадратным единицам.

Изменив положение трех спичек так, как показано на правом рисунке, мы уменьшим площадь фигуры на две квадратные единицы.

Получится многоугольник с площадью, равной четырем квадратным единицам.

Это решение приводится во многих сборниках головоломок.

Имеются и сотни других решений. Существует связь между этой задачей и игрой в полимино, о которой рассказывается в следующей главе. Каждая из пяти фигур тетрамино (состоящих из четырех единичных квадратов каждая) позволяет найти много решений задачи со спичками. Нужно лишь отбрасывать квадраты, заменяя их равновеликими по площади треугольниками до тех пор, пока длина периметра получившейся фигуры не достигнет 12 спичек. Некоторые из таких фигур показаны на рис. 60.

Рис. 60

В каждом стоят фигурки, построенные из одного и того же элемента тетрамино.

Возможно решение в виде звезды (рис. 61).

Рис. 61

Подбирая ширину лучей, можно получать звезду любой площади: от 0 до 11,196 квадратных единиц — площади правильного десятиугольника, наибольшей площади, которую можно ограничить периметром длиной в 12 спичек.

7. Задачу об объеме оставшейся части шара можно решить, не прибегая к высшей математике. Пусть R — радиус шара. Как видно из рис. 62, радиус цилиндрического отверстия равен

а высота сферических шапочек на концах цилиндра равна R — 3.

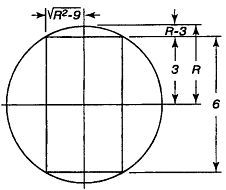
Рис. 62

Для вычисления объема остатка, получающегося после того, как вырезаны цилиндр и шапочки, нужно прибавить объем цилиндра 6π(R² — 9) к удвоенному объему сферической шапочки и вычесть эту сумму из объема шара

Объем шапочки вычисляется по формуле:

где А — высота, а r — радиус.

При вычислении все члены взаимно уничтожаются, кроме 36π.

Это число и равно объему остатка в кубических единицах. Другими словами, объем остатка постоянен, независимо от размера сферы и диаметра отверстия.

Самое раннее упоминание об этой задаче я нашел у С. Джонса.[22] Там же приводится и аналогичная двумерная задача. Если в кольце произвольного размера провести самую длинную прямую линию, то площадь кольца равна площади круга, построенного на этой прямой как на диаметре (рис. 63).

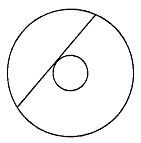
Рис. 63

Некоторые читатели быстро решили задачу с помощью весьма тонкого рассуждения. Редакция журнала не стала бы предлагать задачу своим читателям, если бы та не имела единственного решения. Но коль скоро задача имеет единственное решение, объем оставшейся части шара не зависит от радиуса отверстия и сохраняет свое постоянное значение даже тогда, когда радиус отверстия становится равным нулю. Поэтому объем оставшейся части шара равен объему шара диаметром 6 см, то есть З6π см³.

8. В любой момент времени жуки находятся в вершинах квадрата, который сжимается и поворачивается по мере сближения жуков. Поэтому путь преследователя всегда будет перпендикулярен пути преследуемого. Это значит, что если А приближается к В, то скорость В не имеет компоненты вдоль направления скорости А.

Следовательно, А поймает В через такой же промежуток времени, как если бы В стоял на месте. Длина каждой спирали будет равна стороне квадрата—10 см.

Если же три жука выползают из вершин равностороннего треугольника, то составляющая скорости каждого жука, направленная к его преследователю, будет равна половине всей скорости жука (косинус угла 60° есть 1/2). Поэтому жуки будут сближаться со скоростью 3/2, если за единицу принять скорость жука относительно бумаги. Жуки встретятся в центре треугольника через промежуток времени, равный отношению стороны треугольника к утроенной скорости жука. Каждый жук при этом проползет расстояние, равное 2/3 стороны треугольника.

9. Когда Джон задумался над задачей профессора, ему было известно, что во всех семьях количество детей различно, а всего детей меньше 18. Кроме того, он знал, что если перемножить число детей, то получится номер дома профессора. Поэтому прежде всего он должен был разложить номер дома на множители, сумма которых была бы меньше 18. Если бы это можно было сделать только одним способом, то Джон решил бы задачу сразу. Поскольку он не мог ее решить без дополнительной информации, мы делаем вывод, что номер дома допускает разложение на множители более чем одним способом. Придя к такому заключению, мы должны выписать все возможные комбинации четырех различных чисел, сумма которых не превышает 18, и вычислить произведения каждой четверки.

Оказывается, что во многих случаях одно и то же произведение получается для разных комбинаций чисел. Как же решить, какое из произведений равно номеру дома?

Ключ к решению заключается в вопросе Джона о том, имеет ли самая маленькая семья больше одного ребенка. Этот вопрос приобретает смысл лишь в том случае, если номер дома 120. Разложить это число на множители можно следующими способами: 1x3x5x8, 1х4х5х6 и 2хЗх4х5. Если бы Смит ответил отрицательно, задача оставалась бы нерешенной. Но раз Джон ее все-таки решил, это значит, что ответ был положительным. Поэтому в семьях было 2, 3, 4 и 5 детей.

Глава 12. ПОЛИМИНО

Термин «полимино» ввел в употребление известный математик Соломон В. Голомб. В своей статье «Шахматные доски и полимино»,[23] написанной им еще в бытность его аспирантом Гарварда, Голомб определил полимино как «односвязную» фигуру, составленную из квадратов. Односвязность фигуры означает, что каждый входящий в нее квадрат имеет по крайней мере одну сторону, общую с другим входящим в нее же квадратом. Шахматист, добавляет Голомб, сказал бы, что квадраты составлены «ходом ладьи», потому что ладья могла бы обойти все квадраты полимино за конечное число ходов.

На рис. 64 показаны мономино и все возможные фигуры полимино из двух, трех и четырех квадратов.

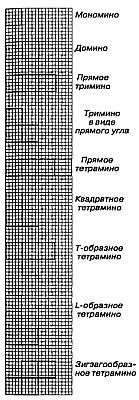
Рис. 64

Существует только один тип домино, два типа тримино и пять типов тетрамино. У пентамино число различных фигур возрастает сразу до двенадцати. Все они показаны на рис. 65.