Рис. 44 Загадочная картинка Лойда «Тедди и львы». На картинке вверху — семь львов и семь охотников, на картинке внизу — восемь львов и шесть охотников.

В 1914 году, через три года после смерти отца, Лойд-младший издал гигантскую «Энциклопедию головоломок», в которой была собрана, несомненно, самая обширная коллекция задач, когда-либо появлявшаяся в одном сборнике. Из этой сказочной, давно уже ставшей библиографической редкостью книги заимствована следующая задача. На ее примере видно, как искусно умел старый мастер переделывать любую, пусть даже самую простую задачу, для решения которой не нужно владеть ничем, кроме умения логически мыслить и обращаться с дробями, превращая ее в захватывающе увлекательную головоломку.

В Сиаме очень ценятся два вида бойцовых рыб: большой белый окунь, называемый королевской рыбой, и маленький черный карп, известный под названием дьявольской рыбки. Эти виды рыб настолько враждуют между собой, что, едва завидев друг друга, бросаются в бой и бьются насмерть.

Королевская рыба легко может справиться за несколько секунд с одной или двумя маленькими рыбками. Но дьявольские рыбки настолько проворны и действуют так слаженно, что втроем не уступят одной большой рыбе, однако не смогут и одолеть ее. Атакуют они так умело и изобретательно, что вчетвером приканчивают большую рыбу за какие-нибудь три минуты. Собираясь в еще большую стайку, они расправляются со своим врагом еще быстрее, причем между продолжительностью схватки и числом рыбок существует прямо пропорциональная зависимость (то есть пять рыбок расправятся с одной королевской рыбой за 2 мин 24 сек, шесть рыбок — за 2 мин ровно и т. д.).

Предположим, что 4 королевские рыбы сражаются с 13 дьявольскими рыбками. Кто выиграет бой и сколько времени он продлится? Предполагается, что дьявольские рыбки действуют наиболее эффективным способом.

Во избежание неоднозначности в условии сформулированной Лойдом задачи следует пояснить, что дьявольские рыбки всегда атакуют группами из трех и более рыб и, напав на королевскую рыбу, дерутся до тех пор, пока не прикончат ее. Мы не можем, например, предположить, что, пока двенадцать дьявольских рыбок осаждают четырех больших рыб, тринадцатая дьявольская рыбка носится туда и обратно, нападая на всех четырех больших рыб одновременно. Если принять предположение о том, что на большую рыбу может нападать не только целая дьявольская рыбка, но и любая ее доля, то рассуждать можно так. Если четыре дьявольские рыбки приканчивают одну королевскую рыбу за три минуты, то тринадцать дьявольских рыбок прикончат ее за 12/13 мин, а четырех королевских рыб — за 48/13 мин (то есть за 3 мин 41 7/13 сек). Но рассуждая точно таким же образом, можно показать, что двенадцать дьявольских рыбок прикончат одну королевскую рыбу за одну минуту, а четырех рыб — за четыре минуты, даже без помощи тринадцатой рыбки. Это заключение, очевидно, противоречит условию Лойда о том, что три дьявольские рыбки не могут совместными усилиями одолеть врага.

Профессор Артур У. Беркс сообщил мне об интересной связи, существующей между лойдовскои игрой в пятнадцать и компьютером. Оба они обладают конечным числом состояний, последовательно сменяющих друг друга. Работа компьютера и решение головоломки начинаются с вполне определенного состояния. Все остальные состояния можно разделить на две группы: «допустимые», реализующиеся при указанных начальных данных, и «недопустимые», которые реализоваться не могут. Эту связь Беркс рассмотрел более подробно в свой книге.[19]

Ответы

В шахматной задаче «белые» объявляют мат в три хода, взяв пешку ладьей. Если черный слон возьмет ладью, то белые переведут своего коня на f3, тем самым вынуждая черных переставить слона. Тогда белые объявляют мат, делая ход пешкой на g4. Если бы черные взяли вместо ладьи коня, белые объявили бы шах ладьей Лh3+, черные в этом случае прикрываются слоном (Ch4), а белые, как и раньше, объявляют пешкой мат на g4.

После того как пуля сбила белого коня, белые, взяв черную пешку пешкой, объявят мат в четыре хода. Если черные сделают ход слоном СеЗ, то белые ответят ладьей Лg4. Далее следует ход черного слона Cg5 и ответный ход белой ладьей Лh4+ (шах). Черный слон берет ладью, а белые объявляют мат пешкой на g4.

После того как пуля сбила с доски белую пешку h2, белые объявляют мат в пять ходов, делая первый ход ладьей Лb7. Если последует ход черных СеЗ, то 2. Лb1 Cg5; 3. Лh + Ch4; 4. Лh2!! gh; 5. g4x (мат).

Если же черные делают первый ответный ход слоном Cg1, то следует: 2. Лb1 Ch2; 3. Ле1 Kph4; 4. Kpg6. На любой ход черных белые отвечают 5. Ле4х (мат).

Если бы первой пулей была сбита белая ладья, а не конь, белые объявили бы мат в шесть ходов, начиная игру конем (Kf3). Тогда лучшим ходом черных был бы ход слоном Ce1, который привел бы к такому продолжению: 2. K: el Kph4; 3. h3 Kph5; 4. Kd3 Kph4; 5. Kf4 h5; 6. Kg6x (мат).

* * *

Наездников можно посадить на ослов (которые при этом словно по волшебству сразу поскачут галопом) таким образом, как это пoказано на рис. 45.

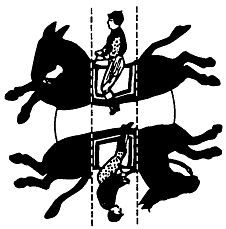
Рис. 45 Решение головоломки с ослами и седоками.

На рис. 46 воспроизведен предполагаемый источник головоломки Лойда: персидский рисунок начала семнадцатого века.

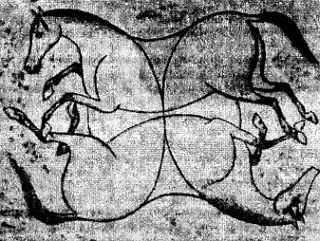
Рис. 46 Персидский рисунок XVII века, послуживший, как предполагают, источником головоломки Лойда.

* * *

Что касается загадочной картинки «Тедди и львы», то бессмысленно спрашивать, который из львов исчез или который из охотников вдруг появился. Когда части смещаются, исчезают все львы и охотники, а вместо них появляются восемь новых львов, каждый на 1/8 меньше первоначального, и шесть новых охотников, каждый на 1/6 больше прежнего.

* * *

Известно много решений задачи о дерущихся рыбах. Вот решение, которое дал сам Лойд.

Четыре маленькие рыбки расправляются за 3 мин с одной большой рыбой, в то время как остальные дьявольские рыбки, разбившись на тройки, нападают на каждую из трех остальных больших рыб. После этого пять рыбок, объединившись, разделываются с еще одной большой рыбой за 2 мин 24 сек. Остальные маленькие рыбки в это время продолжают драться с большими.

Если бы этим рыбкам (они разделились на две группы, так как дерутся с двумя королевскими рыбами) помогала еще одна дьявольская рыбка, то все три группы рыбок кончили бы бой одновременно. Поэтому сил у каждой из оставшихся в живых королевских рыб осталось ровно столько, сколько необходимо, чтобы сражаться с одной дьявольской рыбкой в течение 2 мин 24 сек. Если же на любую из королевских рыб нападает сразу не одна, а семь рыбок, то они приканчивают ее за у этого времени, то есть 20 4/7 сек.

У единственной оставшейся в живых королевской рыбы сил к концу этих 20 4/7 сек хватит только на то, чтобы продержаться еще 20 4/7 сек против одной дьявольской рыбки (напомним, что на нее нападало шесть маленьких рыбок). Все же 13 дьявольских рыбок, объединив свои силы, расправляются с ней за 1/13 этого времени, то есть за 1 53/91 сек.

Сложив продолжительность всех схваток — 3 мин, 2 мин 24 сек, 20 4/7 сек и 1 53/91 сек, мы найдем, что весь бой длился 5 мин 46 2/13 сек.