Поверхности могут быть не только односторонними и двусторонними. С точки зрения топологии, они могут отличаться друг от друга числом своих краев и их устройством. Поскольку ни число краев, ни их структуру нельзя изменить, деформируя поверхность, они называются топологическими инвариантами. Рассмотрим поверхности, имеющие не более двух краев. Будем считать, что краем могут быть либо простые замкнутые кривые, либо кривые, имеющие форму обычного простого узла. При таком предположении можно указать следующие 16 типов поверхностей (сюда не входят такие поверхности без края, как сфера, тор и бутылка Клейна):

Односторонние поверхности с одним краем

1. Край имеет форму простой замкнутой кривой.

2. Край «завязан узлом».

Двусторонние поверхности с одним краем

3. Край — простая замкнутая кривая.

4. Край «завязан узлом».

Односторонние поверхности с двумя краями

5. Оба края — простые замкнутые кривые, не зацепленные друг за друга.

6. Оба края — простые замкнутые кривые, зацепленные друг за друга.

7. Оба края завязаны в узел, но не зацеплены друг за друга.

8. Оба края завязаны в узел и зацеплены друг за друга.

9. Один край простой, другой завязан узлом; между собой края не зацеплены.

10. Один край простой, другой завязан узлом; края зацеплены.

Двусторонние поверхности с двумя краями

11. Оба края — простые замкнутые кривые, не зацепленные друг за друга.

12. Оба края — простые замкнутые кривые, зацепленные друг за друга.

13. Оба края завязаны в узел, между собой не зацеплены.

14. Оба края завязаны в узел и зацеплены друг за друга.

15. Один край простой, другой завязан в узел; друг за друга края не зацеплены.

16. Один край простой, другой завязан в узел; края зацеплены.

Построить бумажные модели всех этих шестнадцати типов поверхностей нетрудно. Модели поверхностей 1 — 12 изображены на рис. 30, а модели остальных четырех поверхностей — на рис. 31.

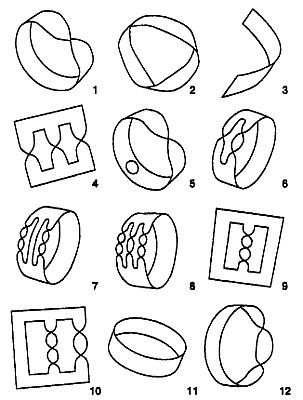
Рис. 30 Бумажные модели поверхностей 1-12.

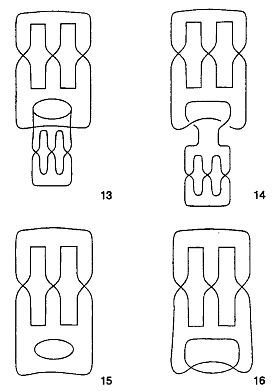
Рис. 31 Бумажные модели поверхностей 13–16.

Если некоторые из этих моделей определенным образом разрезать, то получатся довольно неожиданные результаты. Почти все, кому случалось играть с листом Мёбиуса, знают, что, разрезав его вдоль на две половины, мы получим не два отдельных листа (как можно было бы ожидать), а один большой лист. (Этот большой лист перекручен на четыре пол-оборота, следовательно, из него можно сделать двойной лист Мёбиуса, о котором мы уже говорили.) Менее известно, что если продольный разрез совершать так, чтобы он проходил от края на расстоянии одной трети ширины листа, то, вернувшись в исходную точку, мы обнаружим, что лист Мёбиуса распался на два листа Мёбиуса: большой и сцепленный с ним лист меньших размеров.

Разрезав поверхность 12 на две половины вдоль полоски, мы получим две сцепленные между собой ленты одинаковых размеров, каждая из которых является точной копией разрезанной. При разрезании поверхности 2 на две половины получается большая лента, завязанная узлом. Этому фокусу была посвящена специальная книжка, вышедшая в Вене в восьмидесятых годах прошлого века, которая мгновенно разошлась. В книжке раскрывался секрет, как, не прибегая к магическим трюкам и волшебству, завязать в узел замкнутую ленту.

Когда мы говорим, что два края «зацеплены», мы имеем в виду, что они соединены так же, как два звена в цепи. Чтобы звенья можно было разнять, одно из них необходимо распилить, а через образовавшееся отверстие протащить другое. Однако две замкнутые кривые могут быть зацеплены так, что для того, чтобы их разнять, не обязательно провести одну из них через отверстие в другой. Проще всего это сделать так, как показано на рис. 32 (верхние кривые).

Три замкнутые кривые, изображенные на рис. 32 внизу, нельзя отделить друг от друга, хотя они и не связаны между собой. Если удалить любую из кривых, то две оставшиеся окажутся свободными. Если сцепить любые две кривые, то свободной окажется третья кривая. Иногда такие кольца называют кольцами Борромео, поскольку они были изображены на гербе семейства Борромео, жившего в Италии эпохи Возрождения. Мне не известно, как построить бумажную модель поверхности без самопересечения, у которой два или большее число краев устроены так, что их нельзя разделить, хотя они и не зацеплены. Может быть, кому-нибудь из остроумных читателей удастся построить такую модель.

* * *

Интересную модель двойного листа Мёбиуса можно сделать из жесткого пластика. На такой модели особенно легко описать полный оборот пальцем, просунув его между «двумя» лентами.

Один из читателей предложил изготовить модель из гибкого белого пластика, а затем в промежуток между «полосками» вложить прокладку из красного пластика. Когда красную прокладку вынимают, превращение двух белых лент в одну кажется особенно удивительным, поскольку до этого хорошо было видно, как красная прокладка всюду разделяла то, что можно было принять за две отдельные ленты. Концы красной прокладки нужно не склеивать, а просто накладывать друг на друга, иначе красная лента окажется зацепленной за белую и ее нельзя будет вытащить.

Красная прокладка в такой модели принимает форму листа Мёбиуса. Точно так же всякую неориентируемую (одностороннюю) поверхность можно накрыть так называемой «двулистной» двусторонней поверхностью. Например, бутылку Клейна можно полностью накрыть тором, половина которого должна быть вывернута наизнанку. Как и при накрывании листа Мёбиуса, кажется, что эта поверхность состоит из двух отдельных поверхностей, вложенных одна в другую. Проколов такую поверхность в любой точке, мы обнаружим, что внутренняя поверхность отделена от наружной поверхностью бутылки Клейна. Тем не менее и внутренняя и наружная поверхности являются частями одного и того же тора.[14]

В наши дни редко кому удается придумать математическую игру, которая была бы одновременно и новой и интересной. Именно такой оригинальной и увлекательной является игра в гекс, впервые появившаяся в пятидесятые годы в Институте теоретической физики Нильса Бора в Копенгагене. Гекс вполне может стать одной из наиболее популярных и наиболее полно исследованных математических игр нашего века.

В гекс играют на доске, имеющей форму ромба, составленного из шестиугольников (рис. 33).

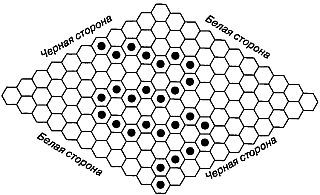
Рис. 33 Игра в гекс на доске со стороной из 11 шестиугольников. Черные выиграли.

Число шестиугольников может быть разным, но обычно предпочитают играть на доске, вдоль стороны которой укладывается одиннадцать шестиугольников. Две противоположные стороны ромба называются «черными», две другие — «белыми». Шестиугольники, находящиеся в углах ромба, относятся к обеим сторонам. Один игрок играет черными фишками, второй — белыми. Играющие по очереди ставят фишку на любой шестиугольник, еще не занятый другой фишкой. Цель «черных» состоит в том, чтобы построить цепь из черных фишек между двумя «черными» сторонами. «Белые» стремятся построить цепь из белых фишек между «белыми» сторонами.