Своеобразие и эволюцию новых методов можно проследить, например, по исследованиям Кеплера и Кавальери. Так, Кеплер при определении целесообразной формы... винных бочек, когда при наименьшей затрате материала требуется получить наибольшую вместимость, разбивал идеальную поверхность изучаемого тела на элементарные части, суммировал их и тем самым непосредственно вводил бесконечно малые величины. Он применял способы исчисления бесконечно малых и в астрономических исследованиях.

Если использование этих способов у Кеплера ограничено конкретными задачами, возникавшими в ходе его научной деятельности, то в поисках более общих и систематизированных принципов образования и измерения поверхностей и тел Кавальери ввел и исследовал абстрактное понятие «неделимых». (Подобно Кавальери и независимо от него стал применять неделимые и Роберваль.) Неделимые у Кавальери — это элементы, из которых состоит площадь или объем того или иного геометрического объекта и размерность которых на единицу меньше размерности рассматриваемого объекта. Так, точка является неделимым для линии, прямая — для плоскости и т. д. При этом, например, площадь какой-то плоской фигуры определялась через уже известную площадь другой фигуры в результате сравнения отрезков прямых линий (неделимых), которыми эти фигуры покрывались.

Торричелли, отмечая особое воздействие метода неделимых на развитие математики, писал: «Несомненно, что геометрия Кавальери есть удивительное по своей экономии средство для нахождения теорем и дает возможность разрешить огромное число, казалось бы, неразрешимых теорем краткими, прямыми, наглядными доказательствами, что невозможно сделать по методу древних. Это — истинно царская дорога среди зарослей математического терновника... Метод Кавальери является действительно научным способом доказательства, всегда идущим путем прямым и свойственным самой природе. Жаль мне древней геометрии, что она либо не знала, либо не хотела признавать учения о неделимых...»

Однако, по замечанию советского историка математики Л. С. Фреймана, метод Кавальери страдал существенными логическими противоречиями: «Одним из таких противоречий является то, что неделимое (линия) имеет на одно измерение меньше числа измерений у площади, а совокупность неделимых уже имеет столько же измерений, сколько площадь!» Действительно, при наложении, скажем, друг на друга плоскостей, толщина которых равна нулю, нельзя получить какой-то объем определенной толщины — суммирование нулей дает в итоге нулевой результат.

В своих исследованиях Паскаль преодолел подобные противоречия: он рассматривал неделимые как однородные с измеряемым объектом бесконечно малые величины, из которых и составлялись интегральные суммы. Для демонстрации приемов Паскаля приведем простой пример, упоминаемый французским исследователем его научного творчества Умбертом. Предположим, что необходимо определить площадь криволинейной трапеции АВСД, составленной прямой AB, перпендикулярами к ней АС и ВД и кривой линией СД (см. рис. 4).

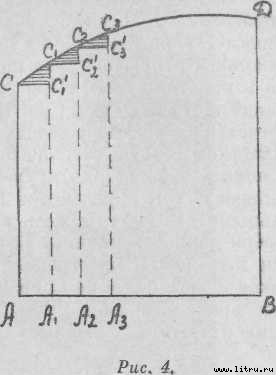
На оси AB берется ряд близко расположенных друг к другу точек A1, A2, A3..., из которых проводятся перпендикуляры к AB до пересечения с СД в точках C1, С2, С3... Из этих точек проводятся отрезки CC'1, С1С'2, С2С'3..., параллельные AB. Если подсчитать и просуммировать площади прямоугольников ACC'1A1, A1C1C'2A2, А2С2С'3А3..., то получится приближенное значение искомой площади, отличающееся от нее на сумму площадей криволинейных треугольников CC1C'1, С1С2С'2, С2С3С'3... (заштрихованных на чертеже). Если же предположить, что точки разделения A1, A2, A3... на AB будут бесконечно увеличиваться в количестве и, следовательно, все более сближаться друг с другом, то получаемые бесконечно узкие прямоугольники и будут неделимыми Паскаля (маленькие заштрихованные треугольники в данном случае уменьшаются и как бы стремятся «раствориться» в кривой СД).

Но Паскаль, пишет Умберт, не удовлетворяется простым интуитивным решением: «Он доказывает строгими методами, что сумма площадей этих маленьких треугольников совсем не влияет на общий результат и ею можно пренебречь, ибо она бесконечно мала по сравнению с суммой площадей прямоугольников. Следовательно, для определения искомой поверхности следует подсчитать сумму площадей этих прямоугольников. Каждая из них в отдельности является бесконечно малой величиной (так как основание каждого прямоугольника бесконечно мало), но число прямоугольников бесконечно велико. Таким образом, речь идет о подсчете сумм бесконечно большого количества бесконечно малых величин, то есть о том, что современные математики называют интегрированием. Интегральное исчисление, по крайней мере в своем начале, было искусством подсчета этих сумм и вычисления с их помощью площадей и объемов».

В работах, связанных с циклоидой, Паскаль сделал шаг вперед по сравнению со своими предшественниками на пути дальнейшего совершенствования и обобщения методов интегрирования. Он преобразовал понятие совокупности Кавальери в понятие суммы. При этом, как пишет известный немецкий историк математики Вилейтнер, Паскаль проводил отчетливое различие между неделимыми и элементарными частями и «существенно более общим образом толковал понятие равенства фигур, чем это позволяло употребительное до того определение Евклида. Именно он считал равными две фигуры, если различие между ними меньше любой данной величины. Паскаль с полной ясностью проник в существо интеграционного процесса, заметив, что всякое интегрирование приводится к определению некоторых арифметических сумм. Паскаль подошел к определению интеграла ближе всех своих современников».

Применяя метод неделимых к различным величинам, преобразуя одни виды суммирования в другие, Паскаль в геометрической форме получил фундаментальные результаты, относящиеся к так называемым криволинейным в двойным интегралам, с помощью наглядных конкретных примеров и ясных доказательств, искусного использования приемов современной ему и античной математики упорядочил многие интеграционные проблемы, освободив их от нечетких и приблизительных решений. До прямого открытия интегрального исчисления Паскалю оставалось сделать лишь шаг — определить формальные операции интегрирования и дать его особый вычислительный алгоритм. Но Паскаль этого шага не сделал. Как и прежде, помешали его «геометризм» и антиалгебраическая настроенность, использование прямых конкретных методов. Поэтому славу первооткрывателей интегрального и дифференциального исчисления делят между собой Ньютон и Лейбниц, хотя некоторые исследователи и причисляют Паскаля к ним, исходя из возможности легкого перевода исключительно геометрических рассуждений Блеза на абстрактный язык анализа бесконечно малых.