Бальмер показал, что если положить n равным 2 и считать, что m принимает значения 3,4,5 или 6, то приведенная формула практически точно воспроизводит искомую последовательность длин волн. Например, если в формулу подставить n = 2 и m = 3, то получается длина волны красной альфа-линии. Однако Бальмер сделал нечто большее. Он не просто воспроизвел длины волн известных четырех линий, которые позднее были названы в его честь серией Бальмера. Он предсказал существование пятой линии для n = 2 и m = 7. Бальмер не подозревал, что Ангстрем, работа которого была опубликована в Швеции, уже открыл такую линию и измерил ее длину волны. Два значения, экспериментальное и теоретическое, совпадали почти идеально.
Ангстрем умер в 1874 году в возрасте пятидесяти девяти лет. Если бы он прожил дольше, он удивился бы, узнав, что Бальмер, использовав свою формулу, предсказал существование других серий спектральных линий для атома водорода. Эти серии попадают в инфракрасную и ультрафиолетовую области спектра. Бальмер просто положил n равным 1, 3, 4 и 5 и, как и в случае n = 2, позволил m принимать ряд других целочисленных значений. Например, Бальмер предсказал, что при n = 3 и m = 4, или 5, или 6, или 7 существует серия линий в инфракрасном диапазоне. Эта серия линий была открыта в 1908 году Фридрихом Пашеном. Все предсказанные Бальмером серии линий были обнаружены, но никто не мог объяснить, почему его формула оказалась правильной. Какой физический смысл могла иметь формула, полученная подбором, путем проб и ошибок?
Позднее Бор скажет: “Как только я увидел формулу Бальмера, мне немедленно стало все совершенно ясно”22. Спектральные линии атома определяются перескоками электронов с одной разрешенной орбиты на другую. Если атом водорода, находящийся в основном состоянии, n = 1, поглощает достаточно энергии, электрон “перескакивает” на орбиту n = 2, соответствующую более высокой энергии. Это значит, что атом находится в нестабильном, возбужденном состоянии и быстро возвращается в стабильное основное состояние, перепрыгнув из состояния с n = 2 в состояние с n = 1. Он может это сделать, только испустив квант энергии, равный разности энергий этих уровней. В данном случае это 10,2 эВ. Длину волны соответствующей спектральной линии можно вычислить, используя формулу Планка E = hν, где ν — частота испускаемого электромагнитного излучения.
Электроны, перепрыгивающие с нескольких более высоких уровней на один и тот же более низкий уровень энергии, приводят к образованию четырех спектральных линий серии Бальмера. Размер излучаемого кванта энергии зависит только от начального и конечного состояния. Именно из-за этого формула Бальмера дает возможность правильно рассчитать длины волн серии спектральных линий, если положить n = 2 и считать, что т поочередно принимает значения 3, 4, 5 или 6. Формула Бальмера позволила Бору рассчитать и другие спектральные серии, которые получаются, если зафиксировать самый низкий энергетический уровень, на который может прыгнуть электрон. Например, если перескоки электрона заканчиваются уровнем n = 3 получается серия Пашена из инфракрасной области спектра, а перескоки, заканчивающиеся на уровне n = 1, генерируют так называемую серию Лаймана в ультрафиолетовой области23.
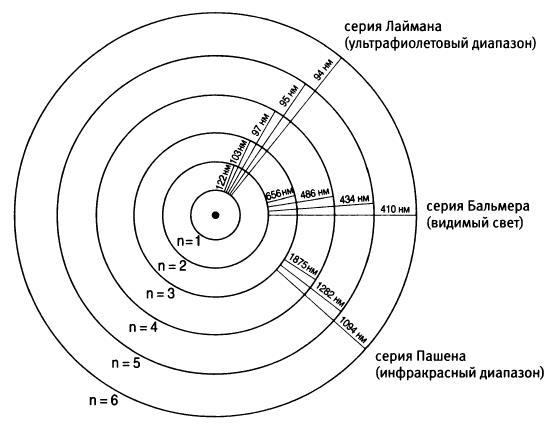
Рис. 7. Энергетические уровни, спектральные линии и квантовые прыжки (рисунок не в масштабе)
Бор обнаружил странную особенность, связанную с квантовыми скачками. Невозможно определить, где во время прыжка находится электрон. Переход между орбитами, энергетическими уровнями, должен происходить мгновенно. Иначе все время перехода с орбиты на орбиту электрон будет излучать энергию. В атоме Бора электрон не может оказаться между орбитами. Как по волшебству он исчезает с одной орбиты и возникает на другой.
“Я абсолютно уверен, что проблема спектральных линий неразрывно связана с вопросом о природе кванта”. Удивительно, но это слова из дневника Планка24. Запись сделана в феврале 1908 года. До появления атома Резерфорда это было все, на что мог решиться Планк, продолжавший борьбу за минимизацию влияния кванта. Бор использовал идею о том, что электромагнитное излучение испускается и поглощается квантами. Но в 1913 году и он еще не мог согласиться с тем, что квантовано само электромагнитное излучение. Даже в 1919 году, когда Планк в своей Нобелевской лекции заявил, что квантовый атом Бора — это “долгожданный ключ, который поможет открыть дверь в удивительную страну” под названием спектроскопия, еще мало кто верил в кванты света Эйнштейна25.
Шестого марта 1913 года Бор отправил Резерфорду первую из трех статей и попросил передать ее в редакцию “Философикал мэгэзин”. В то время (да и еще много лет спустя), чтобы статья молодого ученого была быстро напечатана в английском журнале, ее должен был представить маститый ученый вроде Резерфорда. “Мне не терпится узнать, что вы обо всем этом думаете”, — написал Бор Резерфорду26. Особенно Бора заботила реакция на смешивание квантов с классической физикой. Ответ Резерфорда не заставил себя долго ждать: “Вы проявили большую находчивость в вопросе, касающемся происхождения спектра водорода. Похоже, ваш подход удачен. Но смесь идей Планка со старой механикой очень затрудняет возможность понять, что с точки зрения физики за всем этим кроется”27.
Резерфорду, как и многим другим, трудно было себе представить, как электрон в атоме водорода “прыгает” с одного энергетического уровня на другой. Сложность состояла в том, что в модели Бора нарушался один из основных законов классической физики. Двигающийся по кругу электрон представляет собой колебательную систему: один полный оборот по замкнутой орбите есть осцилляция, а число оборотов за одну секунду — частота осцилляций. Осциллирующая система излучает энергию на частоте, равной частоте осцилляций. Но поскольку в “квантовом прыжке” электрона участвуют два энергетических уровня, мы имеем дело с двумя частотами осцилляций. Резерфорд сокрушался о том, что в теории нет связи между этими частотами, между “старой” механикой и частотой излучения при прыжке электрона с одного энергетического уровня на другой.
Резерфорд указал на еще одну, даже более серьезную, проблему: “Мне кажется, у Вашей гипотезы есть еще одно очень слабое место. Я не сомневаюсь, что Вы и сами это полностью осознаете. Как электрон решает, с какой частотой он будет колебаться, переходя из одного стационарного состояния в другое? Мне кажется, Вы должны были предположить, что электрон заранее знает, где ему надо остановиться”28. Электрон с энергетического уровня п = 3 может перепрыгнуть либо на уровень п = 2, либо на уровень п = 1. Кажется, что электрону, совершающему прыжок, чтобы испустить излучение нужной частоты, надо “знать”, на какой энергетический уровень он направляется. Эти пробелы в теории квантового атома Бор объяснить не мог.
Было еще одно, более мелкое замечание, напугавшее Бора гораздо сильнее. Резерфорд полагал, что “статью следует сократить”, поскольку “длинные статьи отпугивают читателей, которые считают, что у них нет времени вдаваться во все эти подробности”29. Резерфорд предложил исправить английский текст Бора в тех местах, где это необходимо, а в постскриптуме добавил: “Надеюсь, Вы не будете возражать, если я по собственному усмотрению выброшу из статьи то, что мне не представляется необходимым? Жду ответа”30.
Получив письмо, Бор пришел в ужас. Мучительно подбиравшему слова, написавшему множество черновиков, многократно переписавшему статью датчанину мысль о том, что кто-либо (даже сам Резерфорд!) будет менять его текст, казалась кощунственной. Через две недели Бор послал дополненный и переработанный текст. Резерфорд согласился, что изменения “очень хороши и представляются вполне уместными”, однако вновь посоветовал сократить статью. Еще до того, как Бор получил это последнее письмо, он написал Резерфорду, что собирается приехать в Манчестер на каникулы31.