Поначалу этому предположению не отказывают в убедительности. Но уже спустя короткое время математический расчет выносит ей строгий приговор. Оказывается, волновые пакеты, даже в абсолютной пустоте, должны очень быстро расплываться, словно дымовые кольца в воздухе. Даже если долю секунды назад вот здесь была частица — «пакет», то теперь ее уже нет: она размазалась по пространству, как кусок масла, опущенный в кипяток. Однако наука не стоит на месте, безучастно наблюдая, как де-Бройль тщетно пытается наделить голую мысль плотью и кровью. Не проходит и года, как идея де-Бройля дает ростки в целом ряде физических центров мира.
В 1925 году профессор Геттингенского университета в Германии Макс Борн высказывает мысль, что волна де-Бройля — это «волна вероятности». Она определяет вероятность того, что электрон, отразившись от кристалла, попадает в данное место фотопластинки. Она вообще определяет вероятности любых событий, происходящих с электронами и с другими частицами в мире атомов.
Но события не с каждым электроном в отдельности, а с очень большими их группами. Иными словами, волна материи определяет некий статистический закон поведения электронов.
Так ли это? В жизни мы наблюдаем множество статистических закономерностей. Они описывают результаты большого числа одинаковых явлений. При этом несущественно, тысячу раз повторяется явление с одним предметом, или же тысяча предметов один раз демонстрирует это явление.
Можно выпустить тысячу одинаковых пуль по одной мишени одновременно, а можно произвести по той же мишени тысячу выстрелов подряд. Так или иначе, результат окажется почти совершенно одинаковым.
Этот результат состоит в том, что пулевые пробоины распределятся на мишени по вполне определенному закону. Если нет ветра, если пули во всем одинаковы, если у идеального стрелка не дрожит рука, то все пули лягут в десятку. Но, конечно, всегда есть слабые потоки воздуха, две пули всегда в чем-то слегка различны, рука стрелка всегда совершает мелкие непроизвольные движения, которые невозможно точно учесть, столь они случайны. И пули попадут на мишень по закону распределения случайностей.
Этот закон можно изобразить на рисунке. Для этого по одной оси графика надо отложить расстояние от центра мишени до пробоин, а по другой — соответствующие числа пробоин.
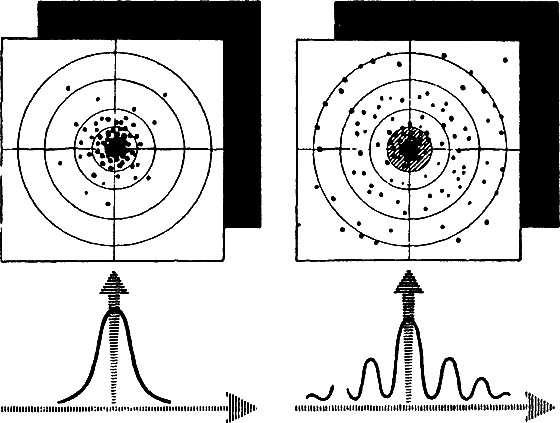
На левом рисунке изображена обычная стрелковая мишень. Если сосчитать число пробоин между окружностями на мишени и отложить эти числа на графике в зависимости от номера окружности, то получится лесенка. Если ее сгладить, то тогда на графике появится кривая Гаусса. На правом рисунке показано, что получилось бы, вздумай мы стрелять по такой мишени электронами. Можно увидеть сразу две интересные особенности. Во-первых, электронные пробоины вышли за заштрихованный контур диафрагмы (она как бы дуло электронного ружья). А во-вторых, показанная внизу кривая не похожа на Гауссову — она спадает волнообразно.
Взгляните на полученный график.
И сравните его с другим. Это график электронного «стрелка». Он получится, если подсчитать так же, как и выше, число электронных «пробоин» на фотопленке. Графики похожи только в одном: кривые спадают по мере удаления от центра. Но вместо монотонного спадания кривой «случайностей» электронная кривая спадает волнообразно.
Вот эту-то волну Борн и предложил считать волной де-Бройля.
Как? Эта «бумажная» волна и есть то, что гордо названо волной материи?
Да, говорит Борн. Волновые свойства электрона должны проявляться тоньше, чем это мыслилось де-Бройлю. Волна теперь «ведет» частицу лишь в том смысле, что электрон взаимодействует с атомами кристалла по «волновому» закону (он и изображен на рисунке).
А этот закон уже дает волновую дифракционную картину электронов на фотопластинке.
Конечно, все это гораздо сложнее, чем вначале полагал де-Бройль. Но волновая картина проявляется на фотопластинке не сразу. Если бросить на кристалл какой-нибудь десяток электронов и затем обработать снимок, то на графике их попаданий никакой закономерности обнаружить не удается.
Что ж, нечего удивляться. Обычная мишень с десятком пулевых пробоин также не позволила бы прийти к закону «случайностей». И тот, и другой — законы статистические, они проявляются тем четче, чем больше число одинаковых явлений.
Все же на нашем снимке можно обнаружить любопытное обстоятельство. Казалось бы, электроны могут попадать лишь в те точки фотопластинки, которые не заходят в «тень» от диафрагмы, поставленной на пути пучка электронов. Вот она заштрихована на рисунке. Однако мы видим, что электроны все же заходят в «запретную» область.
Это очень существенно! Отсюда немедленно следует, что движение электронов подчиняется не старому классическому, а волновому закону. Классический электрон ни в коем случае не нарушил бы строгого запрета и не вышел бы за пределы, очерченные контуром диафрагмы на фотопластинке.
А вот волновой закон, как оказывается, разрешает электрону выходить за эти рамки. Но, правда, с небольшой вероятностью. Однако, какова бы ни была эта вероятность, если только она не равна нулю, то не этот, так другой электрон рано или поздно использует ее.
Это означает, что и сам электрон обладает какими-то необычными, с точки зрения старой физики, свойствами. Свойства эти таковы, что в массе распределение электронов в описываемом явлении оказывается волнообразным.
Что же это за свойства? О них опять же придется отложить разговор. К ним науке тех лет предстоит еще долгий путь.
Единственное, о чем сейчас можно сказать, это то, что новые свойства электрона не позволяют говорить о точном законе движения данного, выбранного для наблюдения электрона. Они не позволяют заранее точно предсказать, в какое место фотопластинки попадет данный электрон. Это можно указать лишь с некоторой степенью вероятности.
Например, в темные кольца на снимке электрон попадает с большей вероятностью, чем в светлые. Эту вероятность новая теория позволяет подсчитать. И при большом числе «попаданий» расчет действительно отлично согласуется с опытом.
Итак, вероятностный закон вместо точного закона классической физики. Не назад ли пошла физика, вместо того, чтобы двигаться вперед?
Нет, недоуменный вопрос не имеет под собой почвы. Если уж говорить об этом, то те «точные» предсказания, которыми старая физика пыталась описывать движение электронов и других микрочастиц, были не более чем миражем.
Классическая физика самонадеянно считала, что она может описать любое явление, любое движение любой частицы в любых условиях. Задай только положение и скорость частицы в некий момент времени и действующие на нее силы, и можно будет сказать все о движении частицы в последующие моменты времени, хоть через миллион лет.
И ученые верили этому без малейшего сомнения. Но с горы видно дальше, чем с холма. «Невежество» классической физики незамедлительно выявилось, как только ученые поднялись на горы теории относительности и теории квантов. Спору нет, «старушка» отлично работает в привычном нам мире больших вещей, движущихся с небольшими скоростями. Но пусть она лучше не суется в мир атомов, мир сверхмалых частиц. Там ее «точные» предсказания — часто попадания пальцем в небо.
«Волны вероятности», вероятностные законы движения сверхмалых частиц — законы куда более точные, чем классические законы в этих масштабах мира. Нет, это не отступление физики, а гигантский скачок вперед!
Но все-таки, что ни говори, а хотелось бы иметь в руках точный закон движения каждой частицы, каждого электрона. Увы, это в нас еще говорит явно устаревшее желание все увидеть, все пощупать. Даже если чего-либо нельзя, и принципиально нельзя ни увидеть, ни пощупать.
Мы живем в «классическом» мире. Все наши образы, представления, все наши мысли в конечном счете черпаются из него.