Так что основное состояние маятника, или состояние с наименьшей энергией, имеет ненулевую энергию в противоположность тому, что можно было ожидать. Оказывается, даже в основном состоянии маятник, как и любая колебательная система, должен совершать минимального размера флуктуации, называемые нулевыми колебаниями. Это означает, что маятник необязательно будет указывать прямо вниз, есть также вероятность обнаружить его отклоненным на небольшой угол от вертикали (рис. 2.10). Подобным образом даже в вакууме, то есть в состоянии наименьшей энергии, волны максвелловского поля не затухают до нуля, но могут иметь небольшие размеры. Чем выше частота (количество колебаний в минуту) маятника или волны, тем больше энергия основного состояния.

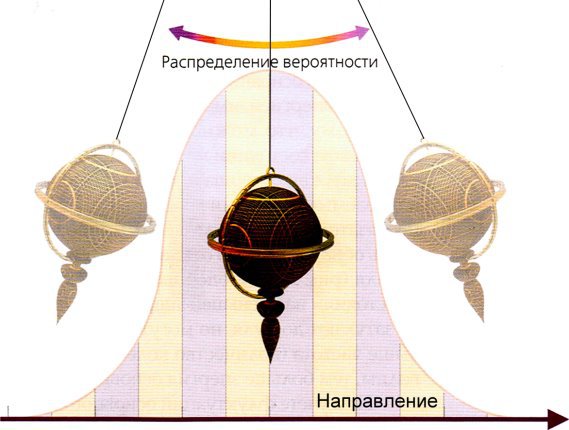
Согласно принципу Гейзенберга маятник не может висеть, указывая строго вниз, и обладать при этом нулевой скоростью. Квантовая теория предсказывает, что даже в состоянии наименьшей энергии он должен испытывать минимальные флуктуации.

Это означает, что положение маятника должно задаваться распределением вероятности. Если он находится в основном состоянии, то с наибольшей вероятностью будет указывать прямо вниз, но имеется также вероятность обнаружить его под небольшим углом к вертикали.

При учете флуктуаций основного состояния в максвелловском поле электрона его видимые масса и заряд оказываются бесконечными, что, конечно, не соответствует наблюдениям. Однако в 1940-х гг. физики Ричард Фейнман, Джулиан Швингер и Синъитиро Томонага разработали согласованный метод устранения, или «вычитания», этих бесконечностей, чтобы иметь дело только с конечными наблюдаемыми значениями масс и энергий[7]. И все же флуктуации основного состояния вызывают небольшие эффекты, которые можно измерить и которые подтверждаются экспериментом. Похожие схемы избавления от бесконечностей работают и для полей Янга — Миллса в теории, которую разработали Чженьнин Янг и Роберт Миллс. Теория Янга — Миллса — это расширение теории Максвелла, которое описывает действие двух других сил, называемых слабым и сильным ядерными взаимодействиями. Однако в случае квантовой теории гравитации флуктуации основного состояния вызывают гораздо более серьезные эффекты. Здесь тоже каждая длина волны имеет свою энергию основного состояния.

Поскольку нет ограничений на то, сколь короткими могут быть длины волн максвелловского поля, то в любой области пространства-времени содержится бесконечное число различных волн и бесконечное количество энергии основного состояния. А вследствие того что плотность энергии, как и вещество, служит источником гравитации, эта бесконечная плотность энергии должна означать, что у Вселенной достаточно тяготения, чтобы свернуть пространство-время в одну точку, чего, однако, очевидно, не происходит.

Можно надеяться разрешить проблему этого внешнего противоречия между наблюдениями и теорией, заявив, что флуктуации основного состояния не влияют на гравитацию, но это не работает. Энергию флуктуаций основного состояния можно обнаружить благодаря эффекту Казимира. Если взять пару металлических пластин и поместить их параллельно друг другу на небольшом расстоянии друг от друга, то число волн различной длины, которые помещаются между пластинами, слегка уменьшится по сравнению с их числом вовне. Это означает, что между пластинами плотность энергии флуктуаций основного состояния хотя и останется бесконечной, окажется меньше плотности энергии вовне на некоторую конечную величину (рис. 2.11). Данная разница в плотности энергии приводит к появлению силы, которая прижимает пластины друг к другу, и эту силу можно наблюдать экспериментально. Силы в общей теории относительности являются источником гравитации наряду с веществом, так что было бы непоследовательным игнорировать гравитационный эффект этой разницы в энергии.

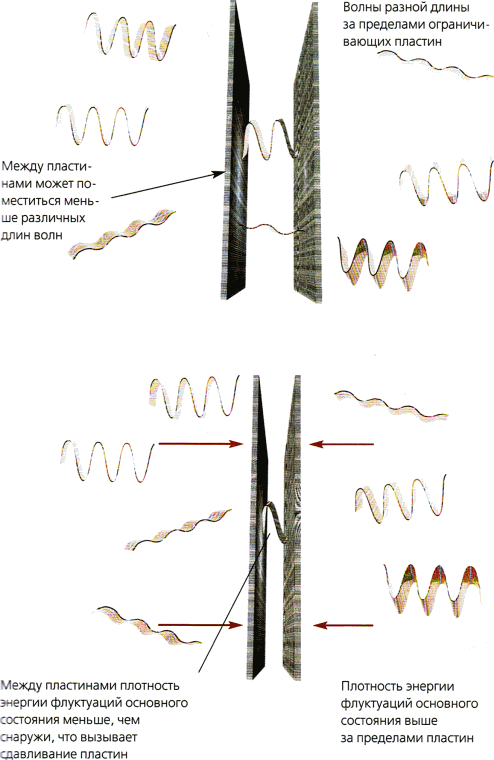
Существование флуктуаций основного состояния было подтверждено экспериментально в эффекте Казимира, который проявляется как небольшая сила, действующая между параллельными металлическими пластинами.

Другой подход к решению рассматриваемой проблемы — попробовать задействовать космологическую постоянную, такую как ввел Эйнштейн в попытке получить стационарную Вселенную. Если эта постоянная имеет бесконечное отрицательное значение, она может в точности скомпенсировать бесконечное положительное значение энергии основного состояния в свободном пространстве, но такая космологическая постоянная кажется слишком искусственным предположением, и к тому же ее величина должна быть подогнана с невероятной точностью.

К счастью, в 1970-х гг. был открыт совершенно новый тип симметрии, который обеспечил естественный физический механизм сокращения бесконечностей, появляющихся из флуктуаций основного состояния. Суперсимметрия — это свойство наших современных математических моделей, которое можно описывать разными способами. Один из подходов состоит в том, чтобы объявить пространство-время имеющим дополнительные измерения помимо тех, с которыми мы знакомы на практике. Они называются размерностями Грассмана, поскольку отсчеты, производимые вдоль них, описываются грассмановскими, а не обычными действительными числами. Обычные числа коммутативны; не имеет значения, в каком порядке вы их перемножаете: 6 умножить на 4 — это то же самое, что 4 умножить на 6. Однако грассмановские величины антикоммутативны: х умножить на у равно — у умножить на х.

Обычные числа А х В = В х А

Грассмановские числа А х В = — В х А

Суперсимметрию впервые стали применять для исключения бесконечностей в материальных полях и полях Янга-Миллса в пространстве-времени, все измерения которого, как обычные, так и грассмановские, были плоскими, а не искривленными. Однако было естественно распространить подход на случай, когда те и другие измерения являются искривленными. Это привело к появлению ряда теорий, называемых супергравитацией, с разной степенью суперсимметрии. Одно из следствий суперсимметрии состоит в том, что у любого поля или частицы должны быть «суперпартнер» со спином либо на 1/2 больше, либо на 1/2 меньше (рис. 2.12).

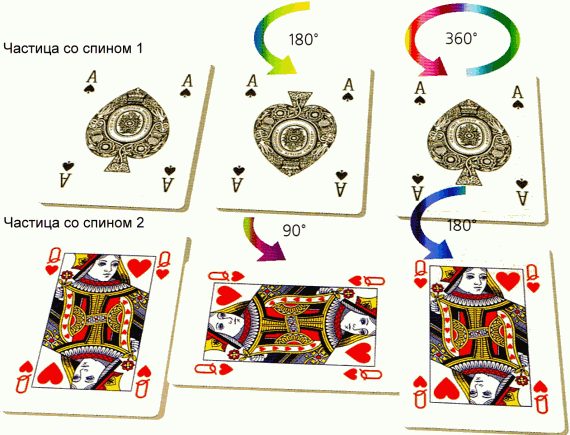
Все частицы обладают свойством, называемым спином, которое проявляется в том, что частицы по-разному выглядят с разных направлений. Это можно проиллюстрировать на примере колоды карт. Возьмем для начала пикового туза. Он выглядит неизменно только при полном обороте — на 360°. Поэтому говорят, что у него спин 1.

С другой стороны, у червовой дамы две головы. И потому она не меняется при повороте на 180°.

Про это говорят: спин 2. Подобным образом можно представить себе объекты со спином 3 и больше, которые не меняются при повороте на меньшие доли полного оборота.

Чем больше спин, тем меньшая доля оборота нужна, чтобы частица в результате осталась неизменной. Но удивительно, что существуют частицы, которые остаются неизменными только после двух полных оборотов. О таких говорят, что они имеют спин 1/2.

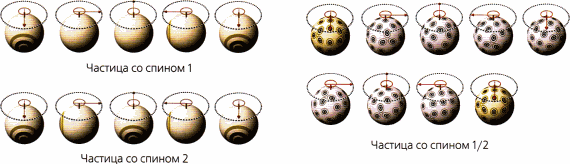
Энергии основного состояния бозонов — полей с целочисленным спином (0,1, 2 и т. д.) — положительны. С другой стороны, энергии основного состояния фермионов — полей, спин которых выражается полуцелыми числами (1/2, 3/2 и т. д.), — отрицательны. Поскольку имеется одинаковое число бозонов и фермионов, крупнейшие бесконечности в теориях супергравитации сокращаются (рис. 2.13).