К середине XIV в. оккамисты сплачиваются в Париже в своего рода научный семинар. Они почти совсем не занимаются теологическими вопросами, на место которых у них все больше выдвигаются проблемы семиотики и математизированного естествознания. Поистине выдающуюся роль в этом интеллектуальном движении парижских оккамистов сыграл Николай Орем (ок. 1320/3/8—1382) родом из Нормандии. В 1348 г. он был принят в Наваррскую коллегию в Париже. Окончив эту коллегию, преподавал в ней до 1361 г. В 1377 г. вступил в должность архиепископа Лизье в Нормандии. Ораторское искусство Орема вызывало зависть многих. Великолепен был и стиль его латинских сочинений. По заказу Карла V он перевел на французский с латинского и прокомментировал ряд сочинений Стагирита на этические, политические и экономические темы.
Орем написал «Трактат о конфигурации качеств» (93), «Трактат о пропорциях», «Трактат о происхождении, природе, преимуществе и обращении денег», а также оставшуюся ненапечатанной рукопись по логической проблеме выводов из понятий (102, 4, 93). В натурфилософии Орема в центре внимания находятся две проблемы (они вообще типичны для номиналистического учения о природе в то время): теория импульса и вопрос об измерении интенсивности величины, формулируемый как учение об интенсификации и ослаблении формы (formae intensio et remissio).
В связи с теорией импульса Орем использовал ставший позднее весьма популярным образ Вселенной как заведенного часового механизма. Вырываясь за пределы традиционной схоластической космологии, он за границами конечной сферической Вселенной перипатетиков помещал некое бесконечное воображаемое пространство. В своей формулировке закона падения тел Орем приближался к галилеевской редакции этого закона. По Орему, воздух есть препятствие для движения падающего тела, скорость которого зависит от сообщенного ему импульса. Отталкиваясь от своей концепции неподвижного неба, Орем принимает тезис об абсолютном движении.
Орем входит в славную плеяду предшественников Коперника, формулируя ряд естественнонаучных (а не теологических, как позднее у Николая Кузанского) аргументов в пользу допущения суточного вращения Земли (и отрицая таковую возможность для неба). Предвосхищая некоторые идеи математического анализа бесконечных малых, Орем оспаривает аристотелевский тезис о том, будто бесконечно большое тело не может обладать конечной тяжестью. По Орему же, напротив, это возможно. Для этого бесконечно большое тело следует представить себе как состоящее из бесконечно большого числа бесконечно убывающих его частей. Эта ситуация мыслилась им возможной в соответствии с математическим (а не собственно физическим) подходом.
Обобщая понятие показателя степени, Орем уже использовал дробные показатели степени, учил о правилах обращения с ними, фактически предвосхищая некоторые законы логарифмической функции. К идее дробной степени мыслитель пришел в процессе проведения сравнений арифметической прогрессии с геометрической. Например, он применял запись вместо современного нам обозначения
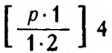
Поворотным пунктом в развитии западноевропейского точного естествознания явилось предвосхищение Оремом метода координат в смысле современной аналитической геометрии в его «Трактате о конфигурации качеств» (впервые издан в 1482 г.). Положим, мы хотим, говорит Орем, построить геометрическую фигуру, фиксирующую изменения такого качества (или «формы»), как теплота, в зависимости от времени. Для этого нам придется за абсциссу (longitudo) взять время, а за ординату (latitudo) — количество теплоты, подлежащее измерению. Начальное значение longitudo представляется перпендикуляром к начальной точке прямой, на которой откладываются значения latitudo.
Иными словами, Орем впервые четко поставил вопрос о количественном измерении субстанциальных форм (это означало прогрессивный сдвиг в схоластической методологии) и об отображении этого измерения в прямоугольной системе координат (что было уже геометрическими средствами для осуществления указанного сдвига). Кривая, получаемая в этой системе, дает наглядную картину изменения интенсивности формы, и в частности фиксирует изменения в «ширине» формы. При этом, по Орему, изменение в непосредственной близости от экстремума является самым медленным. Неопределенная субстанциальная форма схоластиков постепенно превращалась у Орема в однозначное понятие количественно измеримого материального качества, что, естественно, не могло не подготавливать оформление математической теории переменных величин. От Оремовой идеи применения координат открывалась прямая дорога к геометрии Декарта.
Классификация форм («качеств») у Орема весьма далека от схоластических подразделений. Он уже думает над тем, какое применение ей можно найти в физике и механике. Поэтому его классификация оказалась весьма плодотворной. И он делит формы на линейные (с одним измерением), плоские (с двумя измерениями) и телесные (с тремя измерениями). Так, скорость оказывается разновидностью линейного качества, а постоянное и переменное ускорения трактуются как интенсивности скорости. Тем самым физико-механические проблемы формулируются на языке геометрии. Орем вводит специальный термин для обозначения переменного движения (difformis) и рассматривает его в двух видах: равномерно-переменное (uniformiter difformis) и неравномерно-переменное (difformiter difformis). Такая десубстанциалистская трактовка движения делает Орема одним из предшественников галилеевской механики.
Развивая наметившиеся у Оккама скептическую и эмпирическую тенденцию, Орем не считал целесообразным выводить понятие из понятия в отрыве от опыта. Для понимания этого утверждения Орема необходимо иметь в виду, что он толкует понятие как элементарное знание. Фома Брико (XV в.) следующим образом излагает точку зрения Орема: «...ни одно элементарное знание не может быть выведено из другого элементарного знания. Это мнение аргументируется так: никогда какое-либо знание не может быть получено иначе как посредством довода, однако довод есть не что иное, как составное знание...» (102, 4, 93). Правда, аргумент Фомы Брико не совсем оремовский, но его свидетельство весьма важно, так как оно передает мысль из неопубликованной рукописи Орема.
В «Трактате о происхождении, природе, прерогативе и обращении денег» Орем излагает свою доктрину политической экономии. По его мнению, деньги возникают из потребностей обмена товаров: сами по себе деньги не ценность; они лишь общепринятый знак (и здесь семиотическая терминология) для осуществления ценностного обмена. Он резко осуждает государей за порчу монеты; короли не имеют права произвольно завышать курс монет, по своему усмотрению понижая их вес. Политико-экономический трактат был опубликован, однако, только в 1503 г. Есть основания думать, что с его содержанием был знаком Николай Коперник, который в политической экономии мог бы с полным правом считать себя учеником Орема.
Во всяком случае в трудах Коперника по монетному делу, а именно в «Размышлениях» (1517), «Об оценке монет» (1519) и «Трактате о чеканке монет» (1526), очевидно влияние оремовской концепции о гарантиях для строго определенного содержания серебра и золота в монетах фиксированного веса.
Орем был одним из ранних авторов, приступивших к ликвидации монополии латыни как языка научного общения. Он внес исключительно большой вклад в формирование французской философской терминологии (в частности, он ввел такие термины, как materiel, probabilite и др.).
К числу видных оккамистов XIV в. принадлежал также канцлер Оксфордского университета, знаменитый логик и физик Уильям Гейтсбури (ум. в 1380 г.), который в своем труде «Изложение правил для решения софизмов» (ок. 1335) развил ряд положений математической физики. Он описывает ускорение как интенсификацию местного движения. Замедление же есть ремиссия последнего. Так, еще в термины схоластиков Гейтсбури вводит важные понятия положительного и отрицательного ускорения. Согласно Гейтсбури, при равномерно ускоренном или при равномерно замедленном движении скорость нарастает или убывает за равные временные промежутки на равную величину. У Гейтсбури даже можно найти некоторое предвосхищение понятия «мысленный эксперимент», к которому нередко прибегал, в частности, Леопольд Инфельд при разъяснении теории относительности. Существует поразительное сходство трактовки континуума у Гейтсбури с известной аксиомой непрерывности Дедекинда.