0 для 0 или 0,
10 для 1 или 1,
110 для R,
1110 для L,
11110 для STOP.
В качестве примера выпишем команды для машины Тьюринга XN +1 (с дополнительной немой командой 1100 → 00R). Опуская стрелки, цифры, непосредственно предшествующие им, и запятые, получим
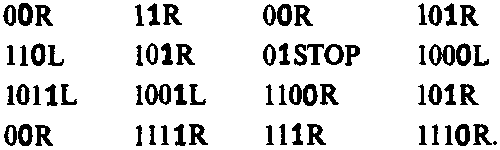
Мы можем улучшить полученный результат, если опустим все 00 и заменим каждые 01 просто единицей в соответствии с тем, что говорилось ранее. Тогда мы получим строку символов
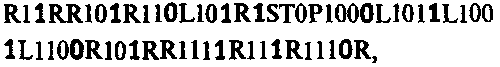
которая на ленте записывается как последовательность
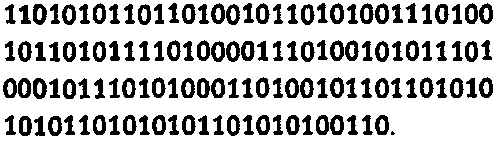
Есть еще два способа немного сэкономить. Во-первых, всегда можно удалить код 110 в начале записи (вместе с бесконечным участком пустой ленты, предшествующим этому коду). Он обозначает последовательность 00R, соответствующую начальной команде 00 → 00R, которую я до сих пор неявно считал общей для всех машин Тьюринга, поскольку она необходима для того, чтобы устройство, начав работу в произвольной точке слева от начала записи на ленте, могло перемещаться вправо до тех пор, пока не встретит первую непустую клетку. Во-вторых, точно так же всегда можно удалить код 110 (и неявную бесконечную последовательность нулей, которая, по предположению, следует за ним) в конце записи, поскольку этой кодовой последовательностью должно заканчиваться описание любой машины Тьюринга (во всех случаях список команд заканчивается командой R, L или STOP). Получающееся двоичное число — это номер машины Тьюринга, который для XN + 1 будет выглядеть так:
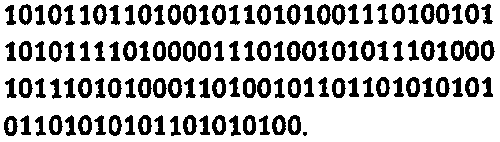
В обычной десятичной записи этот номер равен
450813704461563958982113775643437908.
Иногда машину с номером n мы, не вполне точно, будем называть n-й машиной Тьюринга и обозначать ее Tn . В этом случае XN +1 становится
450813704461563958982113775643437908 — й
машиной Тьюринга!
Кажется поразительным факт, что нам надо пробежать так долго вдоль «списка» машин Тьюринга, чтобы найти машину, выполняющую такую тривиальную операцию, как прибавление единицы к натуральному числу (в расширенном двоичном представлении). (Я не думаю, что моя система кодирования была в целом настолько неэффективна, хотя в ней и есть еще возможности для незначительных улучшений.) В действительности, есть машины Тьюринга и с меньшими номерами, которые представляют интерес, например UN +1 с двоичным номером
101011010111101010,
который в десятичной записи превращается всего лишь в 177 642. Значит, особенно тривиальная машина UN +1, которая просто дописывает 1 единицу в конце последовательности единиц, является 177 642-й машиной Тьюринга. Интересно, что «умножение на два» в списке машин Тьюринга попадает где-то между этими двумя машинами, причем и в унарном, и в расширенном двоичном представлении: номер XN х 2 равен 10 389 728 107, а номер UN х 2 — 1492 923 420 919 872 026 917 547 669.
Наверное, принимая во внимание величины этих номеров, уже не вызовет удивления тот факт, что абсолютное большинство натуральных чисел не соответствует ни одной рабочей машине Тьюринга. Приведем перечень первых тринадцати машин Тьюринга в соответствии с принятой нумерацией:
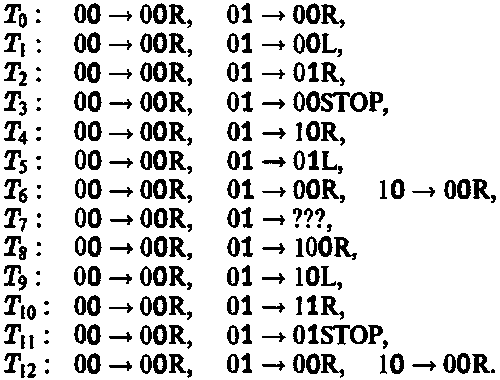
Из этих машин T0 просто перемещается вправо, стирая все, что ей попадается на пути, никогда не останавливаясь и не меняя направления движения. Машина Т1 выполняет в сущности ту же операцию, но более громоздким путем, отступая на шаг назад каждый раз, когда она стирает очередную единицу на ленте. Так же как и T0, машина T2 двигается вправо, никогда не останавливаясь, но относится к ленте более «почтительно», попросту оставляя всю информацию нетронутой. Эти машины не могут использоваться в качестве машин Тьюринга, поскольку никогда не останавливаются. T3 — первая в этом списке «правильная» машина: она скромно прекращает действие после того, как изменяет первую (самую левую) единицу на нуль. T4 сталкивается с серьезной проблемой. Найдя первую единицу на ленте, она переходит во внутреннее состояние, которое нигде не описано, и, следовательно, машина не имеет никаких команд для следующего шага. С той же проблемой сталкиваются T8 , T9 и T10 . С T7 возникают трудности еще более фундаментального характера. Строка нулей и единиц, которой она представляется, включает последовательность из пяти единиц: 110111110. Интерпретации этой последовательности не существует, поэтому T7 намертво застревает сразу же, как только доходит до первой единицы. (Я буду называть T7 , равно как и любую другую машину Tn, двоичное расширенное представлений которой содержит более четырех единиц, некорректно определенной.) Машины T5, T6 и T12 испытывают те же трудности, что и T0, T1, T2: они просто никогда не останавливаются. Все эти машины — T0, T1 , T2 , T5 , T6 , T7 , T8, T9, T10 и T12 — совершенно бесполезные устройства! Только T3 и T11 являются функциональными машинами Тьюринга, да и то не слишком интересными. Причем T11 даже скромнее, чем T3 : натолкнувшись на первую же единицу, она останавливается и вообще ничего не меняет!
Надо заметить, что наш перечень содержит избыточную информацию. Машина T12 идентична T6, а по действиям обе они аналогичны T0, поскольку ни T6, ни T12 никогда не переходят во внутреннее состояние 1. Но нам нет нужды волноваться из-за этой избыточности, равно как из-за изобилия неработоспособных (фиктивных) машин Тьюринга в нашем списке. На самом деле, мы могли бы изменить систему кодирования таким образом, чтобы избавиться от большого числа бесполезных устройств и значительно уменьшить избыточность списка машин. Но все это можно сделать только ценой усложнения нашей примитивной универсальной машины Тьюринга, которая должна расшифровывать вводимую в нее запись и имитировать машину Tn, чей номер она считала. Это было бы оправдано, если бы было можно избавиться от всех бесполезных (и повторяющихся) машин. Но это, как мы увидим чуть позднее, невозможно! Поэтому мы оставим нашу систему кодирования без изменений.
Будет удобно интерпретировать ленту с последовательностью меток на ней, например
…0001101110010000…,
как двоичное представление некоторого числа. Вспомним, что нули простираются бесконечно в обе стороны, а вот количество единиц конечно. Кроме того, я буду полагать, что их число отлично от нуля (т. е. что в этой последовательности существует хотя бы одна единица). Мы можем тогда считывать конечную строку символов между первой и последней единицами (включительно), которая в предыдущем случае имеет вид