— И теперь уже не на октаву, а всего лишь на квинту, — вставил капитан.

— Да, да, — закивал Гиппас, — по-вашему это называется квинтой. Снова отложим на меньшем отрезке струны две трети — получим…

— Опять квинту! — подхватил я.

— Ты определенно делаешь успехи! — просиял Гиппас. — Еще раз разделим таким же способом меньшую часть струны и так далее… Пока не дойдем до конца. И окажется, что на струне, состоящей из семи октав, укладывается двенадцать квинт.

— Подумать только! Точно двенадцать! — восхитился я.

— Гм… — Гиппас помедлил. — В том-то и беда, что не совсем точно. Двенадцать квинт чуть-чуть длиннее семи октав. Правда, разность между ними совсем ничтожна. Это легко подсчитать. Сложим семь октав — семь отрезков струны:

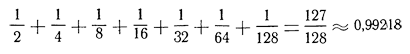
А теперь сложим двенадцать отрезков, образующих квинты:

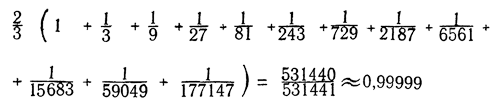
— Остается вычесть из большей суммы меньшую, — сказал я. — 0,99999 — 0,99218 = 0,00781. Да, разность и в самом деле пустяшная.

Гиппас посмотрел куда-то вбок и вздохнул.

— Так-то оно так, и все же… Иногда пустяки портят всю музыку, — невесело пошутил он.

Я хотел спросить, что его так огорчает, да побоялся показаться невежей и поскорее перевел разговор на другую тему.

— Помнится, в ореховом треугольнике есть еще число 4. О нем вы пока ничего не сказали.

— В самом деле, — встрепенулся старик. — Между тем, отношение четырех к трем — 4 : 3 — тоже великолепное. Оно дает… Как это по-вашему? — обернулся он к капитану.

— Кварту, — подсказал тот.

Гиппас поблагодарил его кивком головы и продолжал:

— Так вот, чтобы получить эту самую кварту, надо заставить звучать три четверти струны. И заметьте: октава больше квинты как раз на кварту.

— Ну, это еще надо проверить, — усомнился я.

Бородач насмешливо улыбнулся.

— Кто ж тебе мешает? Раздели отношение 2 : 1 на 3 : 2.

Ну, я, понятно, разделил и получил четыре третьих, чем

очень обрадовал старика.

— Теперь, надеюсь, — сказал он, — ты не сомневаешься, что все четыре числа этого орехового или совершенного, как называл его Пифагор, треугольника находятся между собой в великолепнейших гармонических отношениях.

— Не сомневаюсь, не сомневаюсь, — бодро заверил я, — но что такое октава, кварта и квинта? До конца я этого так и не понял.

Гиппас почесал переносицу.

— Гм, как тебе сказать… Представь себе, что струна это лесенка из сорока двух ступенек. Представил? Прекрасно. Так вот октава — всего лишь восемь ступенек этой лестницы. Оттого, собственно, ее и называют октавой. От латинского окто — восемь. Кварта состоит из четырех ступенек, квинта— из пяти. Названия эти идут опять-таки от латинского кварто и квинто — четыре и пять. А вот разность между квинтой и квартой условились принимать за один музыкальный тон.

— А тон тоже можно выразить числовым отношением? — поинтересовался я.

Оказалось, очень даже можно: стоит только вычислить, во сколько раз квинта (3 : 2) больше кварты (4 : 3 ). Ну, это нам пара пустяков! Я молниеносно разделил отношение 3 : 2 на отношение 4 : 3 и во всеуслышание объявил, что одному музыкальному тону соответствует отношение 9 : 8.

Гиппас назвал меня гениальным ребенком и тут же сообщил, что числа 8 и 9 тоже замечательные. Они входят в другую четверку натуральных чисел — 6, 8, 9 и 12, не менее удивительную, чем 1, 2, 3, 4. Он уж хотел перейти к объяснениям, но я опередил его. Мне захотелось самому разобраться в этой новой четверке, и я довольно быстро подсчитал, что отношение 12 : 6 равно отношению 2 : 1, то есть октаве. Отношение 12 : 8 равно отношению 3 : 2, а это квинта. И, наконец, 12 : 9 равно 4 : 3, или кварте.

После этого Гиппас окончательно расчувствовался.

— Спасибо, друг! Утешил старика! Дай я тебя поцелую,— бормотал он, утирая слезы умиления. — Жаль только, что ты ничего не сказал о числе 9. А ведь это не что иное, как среднее арифметическое между шестью и двенадцатью:

Да и 8 тоже число ничего себе. Можно сказать, превосходное число, хоть и среднее…

— Среднее геометрическое? — предположил я, сгорая от любопытства.

— Среднее гармоническое! — торжественно заявил Гиппас. — Да, есть и такое «среднее» в математике. Иначе говоря, удвоенное произведение двух чисел, деленное на их же сумму. Так вот, 8 — это среднее гармоническое шести и двенадцати:

Я хотел поблагодарить его за новость, но тут он вспомнил, что ничего не сказал о числе 12, тоже весьма любопытном. Потому что именно двенадцать квинт уложил Пифагор в семи октавах. Кажется, он хотел сказать еще что-то, но вдруг спохватился и посмотрел на меня виноватыми глазами:

— Ты устал. Надоел я тебе со своими числами…

— Что вы, что вы! — горячо запротестовал я. — Без числовых отношений мне теперь музыка не музыка!

Не без сожаления покинули мы словоохотливого Гиппаса и отправились обратно на фрегат.

Всю дорогу сопровождала нас чудесная мелодия. Такая плавная, нежная. Жаль, среди приятных звуков нет-нет да попадались фальшивые, вроде волчьего воя. Потом музыка смолкла и голос откуда-то с облаков объявил:

— По просьбе богини Артемиды дельфийской секстет монохордисток исполнил Ноктюрн Пифагора.

— Все-таки молодчина этот Пифагор! — сказал я. — Математик и композитор. Ноктюрны сочинял. Только почему в этом ноктюрне волки завывают?

— Неужели не понимаешь? Все дело в разности, — объяснил капитан. — В маленькой разности между семью октавами и двенадцатью квинтами.

— Но почему волки завывают только в ноктюрнах Пифагора? — не отставал я. — В ноктюрнах Шопена, помнится, никаких волков нет.

Капитан и тут оказался на большой музыкально-математической высоте. По его словам, Шопен писал музыку совсем для другого музыкального строя.

Дело в том, что музыканты давным-давно стремились избавиться от неприятных завываний. Им помогали многие известные математики: Кеплер, Паскаль, Лейбниц, Лаплас, Эйлер…

Но лучше всех справился с задачей органист Андрей Веркмейстер в XVII веке. Он вышел из положения просто и остроумно: чуть-чуть укоротил квинту. И все двенадцать квинт точно уложились в семи октавах. А еще Веркмейстер выровнял интервалы между тонами. Иначе говоря, расположил их равномерно. Это называется темперацией. Так вот, темперация Веркмейстера и стала основой современного музыкального строя.

Первым темперацию принял великий немецкий музыкант Иоганн Себастьян Бах: все знают его замечательное сочинение «Хорошо темперированный клавир». С тех пор новым музыкальным строем стали пользоваться почти все крупные композиторы.

— Почему же «почти», а не все до единого? — заинтересовался я.

— Новое всегда с трудом пробивает себе дорогу, — вздохнул капитан. — Великий Бах принял темперацию сразу, а великий Гендель так никогда и не признал ее.

Как только мы вернулись на фрегат, капитан повел меня в салон и открыл рояль, на котором охотно играл в свободное время.

— Вот инструмент современного строя. Здесь разность звучания между двумя любыми соседними струнами соответствует одному полутону. Квинта, как видишь, состоит из семи полутонов, то есть из трех с половиной тонов. — Он одновременно нажал две клавиши: до и соль. — А в октаве двенадцать полутонов или шесть целых тонов. Если шесть умножить на семь, то есть на число пифагорейских октав, получится 42. То же число получится, если 12 — то есть число квинт в пифагорейской струне — умножить на 3, 5. Вот и выходит, что двенадцать квинт точно укладываются в семи октавах. А теперь давай-ка отложим все двенадцать квинт одну за другой, начиная с нижнего до.