VI

Тарский говорит о больших или меньших дедуктивных системах или классах следствий. Действительно, множество дедуктивных систем (для некоторого языка) частично упорядочено отношением включения, совпадающим с отношением выводимости. Следующее замечание, высказанное Тарским в его работе об исчислении систем, можно использовать как ключ к релятивизации классов следствий, или содержаний, или дедуктивных систем: «среди дедуктивных систем существует наименьшая, то есть являющаяся подсистемой всех других дедуктивных систем. Это система Cn(0)— множество следствий пустого множества. Эта система, которая здесь для краткости будет обозначаться L, может интерпретироваться как множество всех логически верных (valid) предложений (или, в более общем виде, как множество всех тех предложений, которые мы признаем за истинные с самого начала, когда принимаемся строить дедуктивную теорию, являющуюся предметом... нашего исследования)» [310].

Это наводит на мысль, что мы можем использовать вместо нулевой системы L какую-то другую систему «в качестве множества всех тех предложений, которые мы признаем за истинные с самого начала, когда принимаемся строить, и т.д.». Обозначим, как и ранее, дедуктивную систему, содержанием которой мы интересуемся, переменной "A", а «множество всех тех предложений, которые мы признаем за истинные с самого начала», переменной "B". Тогда мы можем написать выражение

как релятивизацию (relativization) Cn(А) Тарского, которое является особым случаем при В= L = Cn(0):

Мы можем писать сокращенно "A,B" вместо "Cn(A,B)", точно так же, как Тарский пишет "A" вместо "Cn(A)".Процитированный отрывок из Тарского подсказывает следующее определение:

Определение: А,В=Cn(А,В) = Cn (A+B) - Cn(B).

А отсюда очевидным образом следует

Ограничиваясь относительным способом записи, мы получаем для истинностного содержания

а для ложностного содержания

что превращает ложностное содержание в относительное содержание, объем (extension) которого совпадает (как первоначально и предлагалось) с классом всех ложных высказываний в А.

VII

 Против предложенного определения ложностного содержания Ар как относительного содержания А₎Ат можно выдвинуть следующее возражение. Это определение интуитивно опирается на цитату из Тарского, в которой Тарский принимает L за наименьшую или нулевую дедуктивную систему. Вместе с тем в нашей последней теореме

мы воспринимали слово «нулевая» слишком буквально: теперь мы видим, что L следует понимать как множество меры нуль, а не как множество, которое, с учетом нашего выражения "-Cn(L)", в буквальном смысле пусто или которого больше нет, согласно нашему определению, поскольку оно было вычтено (так что в A остались только нелогические высказывания, чего мы не имели в виду).

Относимся мы к этому возражению серьезно или нет, оно в любом случае исчезает, если мы решим оперировать с мерой содержания ct(A) или ct(A,B),а не с самим содержанием, или классом следствий Cn(А) или Cn(А,В).

В 1934 году Тарский привлек внимание пражской конференции к аксиоматизации исчисления относительной вероятности дедуктивной системы А при данной дедуктивной системе В, предложенной Стефаном Мазуркевичем[311] и опирающейся на исчисление систем Тарского. Такую аксиоматизацию можно рассматривать как введение функции меры для дедуктивных систем или содержаний А, В, С,... , даже хотя данная конкретная функция — функция вероятности

и возрастает с уменьшением относительного содержания. Это наводит на мысль ввести меру содержания с помощью определения, такого как

Эта функция возрастает и убывает с возрастанием и убыванием относительного содержания. (Возможны, конечно, и другие определения, но это кажется самым простым и очевидным). Мы сразу же получаем:

что соответствует ранее полученным результатам.

Это наводит на мысль, что мы можем ввести понятие правдоподобности, или verisimilitude, высказывания а таким образом, чтобы оно возрастало вместе с возрастанием истинностного содержания этого высказывания и убывало с ростом его ложностного содержания. Это можно сделать несколькими способами [312].

Самый очевидный способ — принять ct(A_t) - ct(A_F) за меру правдоподобности A. Однако по причинам, которые я здесь не буду обсуждать, мне кажется несколько более предпочтительным определить правдоподобность vs(A) как разность, умноженную на некий нормализующий множитель, предпочтительно следующий:

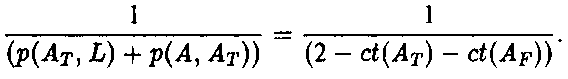
Таким путем мы получаем следующее

Определение:

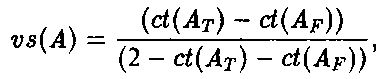
что, конечно, можно переписать в р-нотации как:

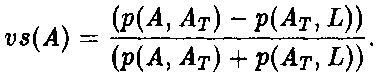
А это приводит к

 и, в частности, к

Иначе говоря, правдоподобность измеряет не ту степень приближения к истине, которой можно достичь, не делая никаких содержательных высказываний (она измеряется нехваткой содержания или вероятностью), а приближение ко «всей истине» — через все большее и большее истинностное содержание. Я полагаю, что правдоподобность в этом смысле является более адекватной целью науки — особенно естественных наук, чем истина, по двум причинам. Во-первых, потому, что мы не думаем, что L составляет цель науки, даже хотя L=L_T. Во-вторых, потому, что мы можем предпочесть теории, которые считаем ложными, другим, даже истинным — таким как L, — если сочтем, что их истинности содержание существенно превышает их ложностное содержание.

В этих заключительных разделах главы 9 я лишь кратко очертил программу сочетания теории истины Тарского с его исчислением систем с целью получить понятие правдоподобности, позволяющее нам говорить — без опасения говорить бессмыслицу — о теориях, являющие лучшими или худшими приближениями к истине. Я, конечно, не предполагаю, что может существовать критерий применимости этого понятия не более, чем может существовать такой критерий для понятия истины. Вместе с тем некоторым из нас (например, Эйнштейну) иногда хочет говорить такие вещи, как например что у нас есть основания предполагать, что эйнштейновская теория тяготения не истинна, но являет лучшим приближением к истине, чем ньютоновская. Иметь возможное со спокойной совестью говорить подобные вещи кажется мне важным пожеланием к методологии естественных наук.

Добавление

Замечание к определению истины по Тарскому^{56}

 В своей знаменитой работе о понятии истины[313] Тарский описывает способ определения понятия истины или, точнее, понятия «x есть истинное высказывание (языка L)».Первоначально этот способ применялся к исчислению классов, но он может применяться в самом общем виде к самым разным (формализованным) языкам, включая языки, позволяющие формализовать некоторые эмпирические теории. Для этого способа характерно то, что определение «истинного высказывания» основывается на определении отношения удовлетворения (relation of satisfaction), или точнее — выражения «бесконечная последовательность f удовлетворяет пропозициональной функции Х»[314]. Это отношение удовлетворения интересно само по себе, вне зависимости от того, что оно играет решающую роль в определении истины (и что шаг от определения удовлетворения к определению истины практически не представляет трудности). Предлагаемые мною замечания связаны с проблемой применения при определении удовлетворения конечных, а не бесконечных последовательностей. Это, по-моему, желательно с точки зрения применения данной теории к эмпирическим наукам, а также и с дидактической точки зрения.