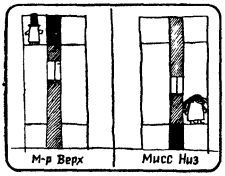
_{Загадка с лифтами решается просто. По вызову мистера Верха сверху могут прийти только лифты, находящиеся в зачерненном участке шахты. Длина этого участка мала по сравнению с длиной остальной, более светлой части шахты. Следовательно, вызванный им лифт с большей вероятностью придет снизу. Так же решается и загадка, мучившая мисс Низ.}

Парадокс с лифтом впервые появился в книге математических задач на смекалку, выпущенной физиком Джорджем Гамовым и его другом Марвином Стерном. Объясняя парадокс с одним лифтом, Гамов и Стерн допустили небольшую ошибку. Они утверждали, что вероятности, «разумеется, останутся такими же», если лифтов будет два или больше.

Первым, кто понял, что это не так, был известный специалист по вычислительной математике из Стэнфордского университета Дональд Кнут. В статье «Задача Гамова — Стерна о лифте»[22] Кнут получил несколько неожиданный результат: с увеличением числа лифтов вероятность того, что на любом этаже (кроме первого и последнего) первым придет лифт снизу, стремится к 1/2, и вероятность того, что первым придет лифт сверху, также стремится к 1/2.

В действительности эта ситуация еще более парадоксальна, чем в первоначальном варианте задачи.

Результат Кнута означает, что если вы находитесь на одном из последних этажей и стоите перед дверями одного из лифтов, то с высокой вероятностью именно тот лифт, который вы ждете, придет снизу, рели же вы готовы сесть в любой лифт, который остановится на вашем этаже, то вероятность того, что первым придет лифт снизу, будет иной. При неограниченном увеличении числа лифтов эта вероятность стремится к 1/2. То же верно и относительно лифтов, приходящих по вызову на нижние этажи сверху.

Разумеется, мы предполагаем, что лифты ходят независимо, с постоянной скоростью и что среднее время ожидания одинаково для всех этажей. Если число лифтов невелико, то вероятности изменяются незначительно. Но если число лифтов достигает 20 или более, то вероятности для всех этажей, кроме первого и последнего, мало отличаются от 1/2.

_{У одного парня были две знакомые девушки, и он никак не мог выбрать, с кем из них отправиться на свидание. Одна из девушек жила к востоку от того места, где жил он сам, другая — к западу.}

_{Ежедневно парень в случайное время спускался на станцию метро и садился в первый попавшийся поезд.}

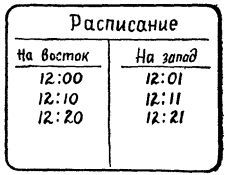
_{Поезда в восточном и западном направлениях шли с интервалом в 10 мин.}

_{Девушка, жившая к востоку от того места, где обитал наш сердцеед, сказала ему как-то раз на прощание.}

_{На следующий вечер девушка, жившая к западу от дома нашего героя, сердито упрекнула его.}

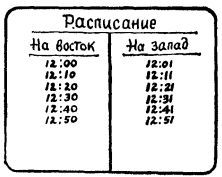
_{Необъяснимое на первый взгляд предпочтение парня к поездам восточного направления напоминает парадокс с лифтами. Хотя поезда восточного и западного направлений идут с интервалами в 10 мин, расписание составлено так, что поезд западного направления прибывает и отправляется на 1 мин позже, чем ближайший поезд восточного направления.}

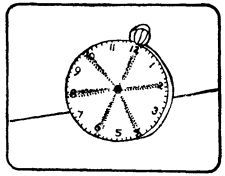
_{Чтобы попасть на поезд, идущий на запад, парень должен ел на станции в течение одного из минутных интервалов, отмеченных на циферблате темными полосами.}

_{Чтобы попасть на поезд, идущий на восток, он должен прибыть на станцию в течение любого из девятиминутных интервалов, заключенных между темными полосами.}

_{Вероятность поехать на запад составляет 1/10, вероятность отправиться на восток составляет 9/10.}

В этом парадоксе время ожидания между поездами задано расписанием. В последовательности случайных событий «среднее время ожидания» между событиями мы получим, просуммировав времена ожидания и разделив полученную сумму на n. Например, среднее время ожидания для поезда, идущего на восток, в нашем рассказе составляет 4^1/2 мин, а среднее время ожидания для поезда, идущего на запад, — всего 1/2 мин.

С временами ожидания связаны и многие другие парадоксы. Возможно, вам понравится следующий.

Если вы бросаете монету, то среднее время ожидания «орла» (или «решки») равно 2 бросаниям. Это означает, что, взяв перечень исходов длинной серии бросаний монеты и подсчитав времена ожидания, отделяющие выпадение одного «орла» от выпадения следующего «орла», вы получите среднее «расстояние» между «орлами», равное 2 бросаниям (если серия начинается не с «орла», то длина серии «решек» до выпадения первого «орла» в расчет не принимается).

Предположим, что на длинном листе бумаги сверху вниз выписаны исходы длинной серии бросаний монеты. Выберите наугад зазор между двумя последовательными бросаниями (например, зажмурьте глаза и проведите по листу горизонтальную черту). Найдите ближайший к проведенной черте «орел» сверху и снизу и подсчитайте число испытаний, отделяющих один «орел» от другого. Повторите эту операцию многократно. Чему будет равно среднее расстояние между «орлами»?

Интуитивно кажется, что «орлы» должны быть в среднем разделены двумя бросаниями. В действительности в среднем их разделяют три бросания.

Причина та же, по которой любвеобильный парень обычно садился в поезд, идущий на восток. Одни серии испытаний между последовательными «орлами» короткие, другие — длинные. Случайно проведенная линия аналогична случайному выбору момента прибытия парня на станцию. Попасть в более длинную серию вероятнее, чем в более короткую.

Приведем теперь простое доказательство того, что три испытания — действительно правильный ответ на вопрос задачи. Монеты «не помнят» исходов предыдущих бросаний, поэтому, где бы вы ни провели черту, среднее время ожидания до выпадения следующего «орла» должно быть равно 2 бросаниям. То же соображение применимо и к среднему времени ожидания, если мы «обратим» всю серию испытаний и будем считать времена ожидания не вперед, а назад. Следовательно, «средняя длина свободного пробега» между «орлами» равна 2х2, то есть 4, если мы будем считать и те бросания, при которых выпали сами «орлы». А так как мы условились понимать под временем ожидания длину серии испытаний, включающую выпадение следующего «орла», но не включающую выпадение предыдущего «орла», то средняя длина свободного пробега равна 4–1 = 3 бросаниям.

Еще более поразительна аналогичная задача с колесом рулетки. В колесе имеются 38 гнезд с номерами, среди которых есть 0 и 00. Следовательно, среднее время ожидания для любого числа, например для 7, равно 38 запускам колеса. Но если вы возьмете запись длинной серии номеров, выпавших при игре в рулетку, и, проводя наугад черту, начнете подсчитывать среднюю «длину свободного пробега» между двумя последовательными семерками, то она окажется равной не 38, а (2 х 38) — 1 = 75.