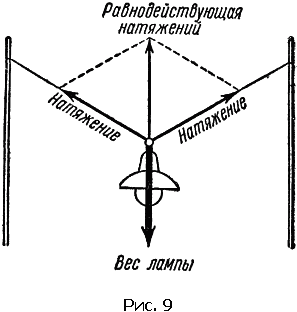
Такое построение называется разложением силы. Всякое число можно представить бесконечным множеством способов в виде суммы двух или нескольких чисел; то же можно сделать и с вектором силы: любую силу можно разложить на две силы – стороны параллелограмма, – из которых одну всегда можно выбрать какой угодно. Ясно также, что к каждому вектору можно пристроить любой многоугольник.

Часто бывает удобным разложить силу на две взаимно перпендикулярные – одну вдоль интересующего нас направления и другую перпендикулярно к этому направлению. Их называют продольной и нормальной (перпендикулярной) составляющей силы.

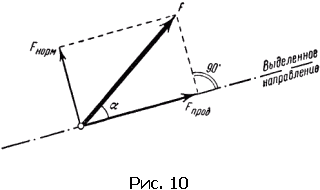
Составляющую силы по какому-то направлению, построенную разложением по сторонам прямоугольника, называют еще проекцией силы на это направление.

Ясно, что на рис. 10

F ²= F _прод ²+ F _норм ²,

где F _проди F _норм– проекция силы на выбранное направление и нормаль к нему.

Знающие тригонометрию без труда установят, что

F _прод= F·cos α,

где α – угол между вектором силы и направлением, на которое она проецируется.

Очень любопытным примером разложения сил является движение корабля под парусами. Каким образом удается идти под парусами против ветра? Если вам приходилось наблюдать за парусной яхтой в этом случае, то вы могли заметить, что она движется зигзагами. Моряки называют такое движение лавированием.

Прямо против ветра идти на парусах, конечно, невозможно, но почему удается идти против ветра хотя бы под углом?

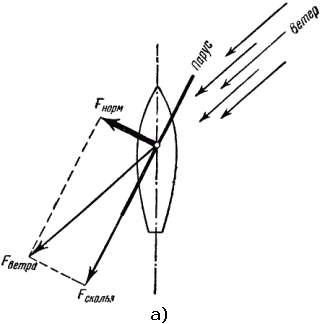
Возможность лавировать против ветра основывается на двух обстоятельствах. Во-первых, ветер толкает парус всегда под прямым углом к его плоскости. Посмотрите на рис. 11, а: сила ветра разложена на две составляющие – одна из них заставит воздух скользить вдоль паруса, другая – нормальная составляющая – оказывает давление на парус. Во-вторых, лодка движется не туда, куда ее толкает сила ветра, а туда, куда смотрит нос лодки.

Это объясняется тем, что движение лодки поперек килевой линии встречает очень сильное сопротивление воды. Значит, чтобы лодка двигалась носом вперед, надо, чтобы сила давления на парус имела бы составляющую вдоль килевой линии, смотрящую вперед.

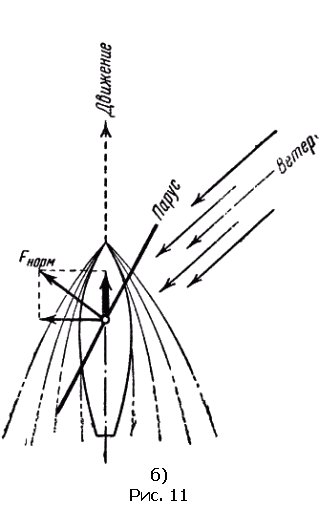
Теперь рис. 11, б, на котором изображена идущая против ветра лодка, должен стать понятным вам. Парус устанавливают так, чтобы его плоскость делила пополам угол между направлением хода лодки и направлением ветра.

Для того чтобы найти силу, которая гонит лодку вперед, силу ветра придется разложить дважды. Сначала вдоль и перпендикулярно к парусу – имеет значение лишь нормальная составляющая, затем эту нормальную составляющую надо разложить вдоль и поперек килевой линии. Продольная составляющая и гонит лодку под углом к ветру.

Наклонная плоскость

Крутой подъем труднее преодолеть, чем отлогий. Легче вкатить тело на высоту по наклонной плоскости, чем поднимать его по вертикали. Почему так и насколько легче? Закон сложения сил позволяет нам разобраться в этих вопросах.

На рис. 12 показана тележка на колесах, которая натяжением веревки удерживается на наклонной плоскости. Кроме тяги на тележку действуют еще две силы – вес и сила реакции опоры, действующая всегда по нормали к поверхности, вне зависимости от того, горизонтальная поверхность опоры или наклонная.

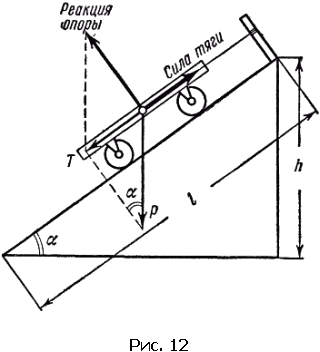
Как уже говорилось, если тело давит на опору, то опора противодействует давлению или, как говорят, создает силу реакции.

Нас интересует, в какой степени тащить тележку вверх легче по наклонной плоскости, чем поднимать вертикально.

Разложим силы так, чтобы одна была направлена вдоль, а другая – перпендикулярно к поверхности, по которой движется тело. Для того чтобы тело покоилось на наклонной плоскости, сила натяжения веревки должна уравновешивать лишь продольную составляющую. Что же касается второй составляющей, то она уравновешивается реакцией опоры.

Найти интересующую нас силу натяжения каната Tможно или геометрическим построением или при помощи тригонометрии. Геометрическое построение состоит в проведении из конца вектора веса Pперпендикуляра к плоскости.

На рисунке можно отыскать два подобных треугольника. Отношение длины наклонной плоскости lк высоте hравно отношению соответствующих сторон в треугольнике сил. Итак,

Чем более отлога наклонная плоскость ( h/ lневелико), тем, разумеется, легче тащить тело вверх.

А теперь для тех, кто знает тригонометрию: так как угол между поперечной составляющей веса и вектором веса равен углу α наклонной плоскости (это углы со взаимно перпендикулярными сторонами), то

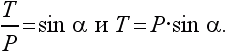
Итак, вкатить тележку по наклонной плоскости с углом α в sin α раз легче, чем поднять ее вертикально.

Полезно помнить значения тригонометрических функций для углов 30, 45 и 60°. Зная эти цифры для синуса (sin 30° = 1/2; sin 45° = sqrt(2)/2; *5sin 60° = sqrt(3)/2), мы получим хорошее представление о выигрыше в силе при движении по наклонной плоскости.

Из формул видно, что при угле наклонной плоскости в 30° наши усилия составят половину веса: T= P·(1/2). При углах 45° и 60° придется тянуть канат с силами, равными примерно 0,7 и 0,9 от веса тележки. Как видим, такие крутые наклонные плоскости мало облегчают дело.

II. Законы движения

Разные точки зрения на движение

Чемодан лежит на полке вагона. В то же время он движется вместе с поездом. Дом стоит на Земле, но вместе с ней и движется. Про одно и то же тело можно сказать: движется прямолинейно, покоится, вращается. И все суждения будут верны, но с разных точек зрения.

Не только картина движения, но и свойства движения могут быть совсем разными, если их рассматривать с разных точек зрения.

Вспомните, что происходит с предметами на пароходе, попавшем в качку. До чего они непослушны! Пепельница, поставленная на стол, опрокинулась и стремительно понеслась под кровать. Плещется вода в графине, и лампа колеблется, словно маятник. Без каких-либо видимых причин одни предметы приходят в движение, другие останавливаются. Основной закон движения, мог бы сказать наблюдатель на таком пароходе, состоит в том, что в любой момент времени незакрепленный предмет может отправиться в путешествие в любом направлении с самой различной скоростью.

Этот пример показывает, что среди различных точек зрения на движение имеются явно неудобные.

Какая же точка зрения наиболее «разумная»?

Если бы вдруг, ни с того ни с сего, лампа на столе наклонилась или пресс-папье подпрыгнуло, то вы подумали бы сначала, что это вам почудилось. Если бы эти чудеса повторились, вы настойчиво стали бы искать причину, которая выводит эти тела из состояния покоя.