Мы привыкли считать, что электроны в атоме движутся по орбитам — под действием электрического притяжения ядра, забывая, что сами на практике, — в ускорителях частиц, плазменных установках и индукционных печах — задаём круговые движения электронов с помощью магнитных полей. В своей работе 1908 г. "Атомные магнитные поля и спектральные серии" Ритц убедительно показал, что только силами магнитной природы можно объяснить спектры излучения атомов. Согласно ему, магнитное поле атома создано набором последовательно соединённых элементарных магнитиков стандартного размера a, образующих вытянутый магнитный стержень (Рис. 94). Вместо магнитов можно взять витки с током, составляющие катушку индуктивности, соленоид с постоянным шагом витка a. Как показал Ритц, в зависимости от числа магнитов (витков) стержень создаёт такие магнитные поля, в которых электрон должен колебаться с теми частотами, что были найдены в спектре атома водорода.
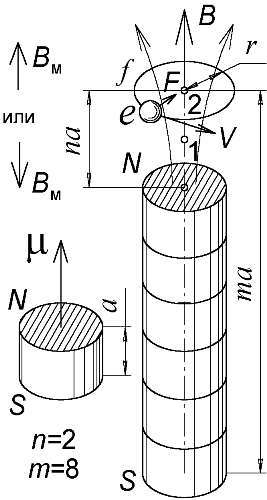
Рис. 94. Магнитная ось, набранная из магнитов, управляет полётом электронов.
При всей кажущейся наивности представления атома в виде некоего прибора (гибрида циклотрона и магнитной антенны), модель Ритца не только верно описала водородный спектр и эффект Зеемана, но и предсказала новые спектральные серии водорода и других элементов, поздней действительно открытые. Но трагическая ранняя гибель Ритца в 1909 г., спустя год после публикации его баллистической теории и модели атома, позволила о них забыть, хотя открытыми с их помощью принципами учёные не побрезговали и пользуются ими до сих пор. В свете открытий ушедшего столетия, которое не внесло ясности в квантовую модель атома, а лишь запутало её, модель атома Ритца обретает новое звучание и смысл.
Так, открыли, что у каждого электрона есть стандартный магнитный момент μ, наделяющий электрон свойствами элементарного магнитика. Тем же магнитным моментом μ обладает и открытый в 1932 г. антиэлектрон, — позитрон. Представим теперь, что позитрон соединился с электроном, и этот диполь стал одним концом притягивать электроны, а другим — позитроны. В итоге, электроны и позитроны, последовательно цепляясь друг за друга паровозиком, могут сливаться в протяжённые прямые цепи, в которых все магнитики (магнитные моменты) электронов и позитронов ориентированны одинаково. Расстояния между их центрами окажутся постоянными, одинаковыми: порядка размера электрона a(Рис. 95). Как было показано (§ 1.16), при контакте электронов с позитронами они вовсе не уничтожаются, а просто слипаются в нейтральную частицу, оказываясь разделены расстоянием, равным классическому радиусу электрона.
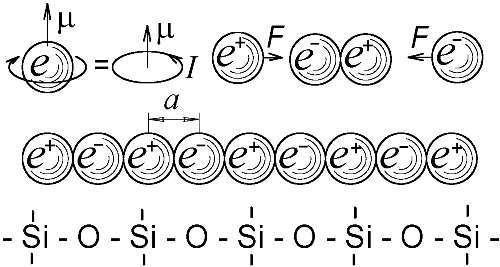
Рис. 95. Магнитный момент электрона как результат вращения. Слияние электронов с позитронами в цепочки типа линейных молекул силикона и игольчатых кристаллов.
Итак, магнитные стержни, оси, набранные из элементарных магнитиков, которые Ритц только предполагал, в принципе могут вырастать сами, подобно кристаллам соли из чередующихся ионов Na+ и Cl-, или линейным молекулам полимеров, построенным из тысяч одинаковых звеньев, к примеру, — из чередующихся атомов Si и O (силикон). Стержни, содержащие равное число электронов и позитронов, не имели бы заряда, но породили бы заметное магнитное поле. Поэтому, оказавшийся возле стержня электрон не был бы ни отторгнут, ни притянут, но мог бы совершать в магнитном поле стержня круговые движения возле точки равновесия с частотой f, не зависящей от его скорости Vи радиуса орбиты r(Рис. 94). В магнитном поле с индукцией Bна электрон с зарядом eи массой Mдействует сила Лоренца F= eVB, заставляющая его двигаться по окружности с центростремительным ускорением ar= V2/ r. Поскольку Ma r= F, имеем MV 2/ r= eVB, откуда угловая скорость электрона 2π f=V/ r= Be/ M. То есть, частота f= Be/2π Mобращения электрона, равная частоте излучаемого им света, зависит лишь от индукции поля B, поскольку величина e/2π Mпостоянна.
Однако, спектры излучения атомов состоят из дискретного ряда частот. Значит, и поле Bможет принимать лишь определённые значения. Это заставило Ритца предположить, что электрон способен занимать в атоме лишь некоторые устойчивые положения, каждому из которых присуще своё значение поля B, задаваемое расстоянием электрона до стержня. Эту мысль о наличии в атоме устойчивых положений и орбит электрона, Ритц, в отличие от Бора, развивал в рамках классического, а не квантового подхода. Он считал, что раз стандартны расстояния и размеры aмагнитов, то тем же расстоянием aдолжны быть отделены и возможные, разрешённые положения электрона — узлы 1, 2, 3…, где он способен пребывать (Рис. 94).
Именно так и вёл бы себя электрон возле электрон-позитронного стержня, который за счёт неравномерного (дискретного) распределения зарядов создаёт небольшое продольное электрическое поле. Поэтому, где бы ни находился электрон, он всегда стремится встать против положительного позитрона, а возникающая при смещении электрона продольная сила возвращает его на место (Рис. 96). То есть, электрон способен устойчиво занимать положения — лишь напротив позитронов, и может "прыгать" вдоль стержня только на расстояние 2 a.
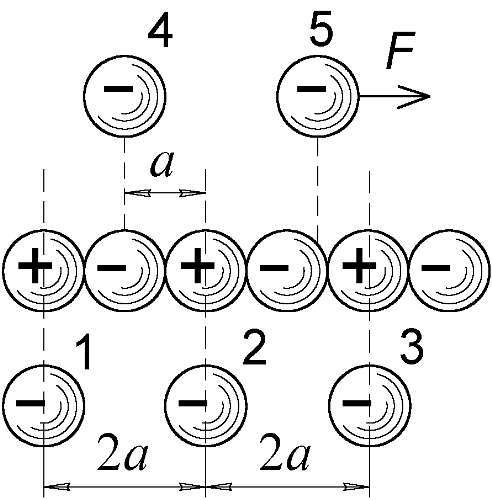
Рис. 96. Устойчивые (1, 2, 3) и неустойчивые (4, 5) положения электрона возле цепочки.
Но смещение электрона вдоль стержня не влияет на величину магнитного поля. Да и Ритц считал, что у электрона кратно аменяется расстояние до магнита. Поэтому, приходим к выводу, что в атоме не один, а два стержня, две магнитных оси, соединённых перпендикулярно, наподобие перекладин креста (Рис. 97). Электрон, размещаясь против позитронов каждой оси, должен находиться в одном из узлов сетки, образованной линиями уровня позитронов, и его расстояние до каждого стержня будет кратно 2 a. Потому, и поле Bменяется прерывисто. Итак, в крестовой магнитной модели атома электрон и впрямь может занимать лишь некоторые устойчивые положения, возле которых и колеблется в магнитном поле крестовины. И, что очень важно, эта дискретность вводится в рамках классической физики. Подробнее о причинах устойчивости таких положений электронов расскажем далее (§ 3.2, § 4.14).
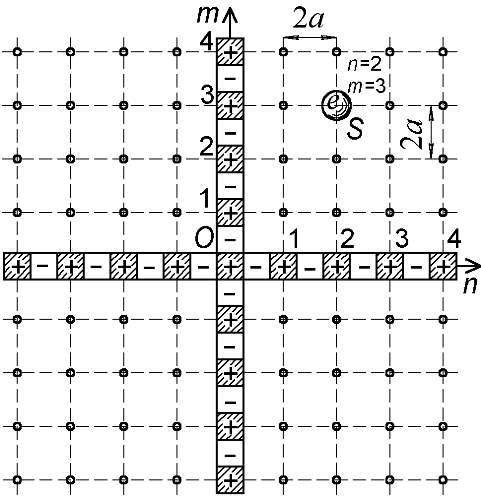
Рис. 97. Сетка и узлы, в которых могут находиться электроны в крестовине.
Крестовины могут нарастать так же естественно, как отдельные стержни. Крест мог бы образоваться из двух "слипшихся" стержней. Но, скорее, электрон-позитронные цепочки, стержни, оси и кресты растут, "кристаллизуются" от неких центров, ядер, подобно тому, как это происходит с настоящими кристаллами, дендритами, и, особенно, — снежинками, симметрично нарастающими от неких центров и ядер кристаллизации. Этими центрами могут быть ядра атомов, их протоны и нейтроны. Тем более, что они, как покажем (§ 3.9), могут содержать тысячи позитронов и электронов; в нейтроне их поровну, а у протона позитронов на один больше. Именно ядра могут поставлять необходимые для роста крестовины частицы.
При "кристаллизации" креста, как и при росте поликристаллов железа, магнитные моменты частиц поначалу ориентируются случайным образом. Но, если в одном стержне случайно окажется чуть больше частиц с моментом, направленным вверх, то его магнитное поле заставит некоторые частицы второго стержня повернуться так, чтобы их моменты, ориентируясь вдоль линий поля, направились вниз. Тогда, и этот стержень создаст поле, в свою очередь побуждающее больше частиц первого стержня повернуться вверх. И так постепенно, путём подобной самоорганизации, магнитные моменты обоих стержней упорядочатся, так что первый стержень образует в плоскости креста поле направленное вниз, а второй — вверх (Рис. 98). В действительности, такая модель атома имеет много общего с первой моделью атома Дж. Дж. Томсона [49, 50], а также с реально наблюдаемой в опытах самоорганизацией магнитных систем. Ведь Томсон исходно строил как раз структурную модель атома, основываясь на ныне незаслуженно забытых опытах с плавающими магнитами, выполненных А. Майером ещё в конце XIX в. [50].