Рассмотрим опыт с продлением жизни частиц, называемых мю-мезонами [54]. В теории относительности скорость мезона находят по его кинетической энергии E, связанной со скоростью релятивистской формулой E= mv 2/2(1– v 2/ c 2) 1/2, где m— масса мезона в покое. Реальная же его скорость Vдолжна вычисляться по классической формуле E= mV 2/2, откуда V=v/(1– v 2/ c 2) 1/4. Если в формуле t=L/Vскорость Vзаменить её выражением через v, получим L/v= t'=t/(1– v 2/ c 2) 1/4, то есть формулу, похожую на формулу СТО для преобразования масштаба времени: t'=t/(1– v 2/ c 2) 1/2. Некоторое несоответствие показателя степени возникает лишь от способа определения энергии Eчастиц.
Значит, продление жизни частиц — это иллюзия, вызванная ошибочностью формул СТО, связывающих скорость и энергию, и исчезающая, если Vопределять классически. Таким образом, здесь снова сталкиваемся с циклическим доказательством справедливости СТО, — доказательством, опирающимся само на себя. Сначала по СТО полагают, что скорость частиц не превосходит скорости света, и из её ложных формул для энергии и массы находят ошибочную скорость, а потом из этой заниженной скорости получают выросшее время жизни частиц. Но, тогда, выходит, и опыт был совсем ни к чему — и без него было ясно, что растяжение времени жизни — это следствие второго постулата СТО о постоянстве скорости света и невозможности её превысить. Такой порочно-круговой метод доказательства имел место почти во всех релятивистских опытах, которые толковали всегда с позиций теории относительности. Понятно, что ничего, кроме её подтверждения, тогда и не получится. Если же теория относительности ложна и возможны сверхсветовые частицы, то все эти доказательства, в том числе доказательство растяжения времени жизни, — ничего не стоят.
И такие сверхсветовые частицы, действительно, неоднократно наблюдались в экспериментах. Ещё в 1908 г. Ритц полагал, что среди электронов, рождённых распадом радия, есть сверхсветовые, если судить по оставляемому ими в опыте Кауфмана следу на экране [8]. Не раз фиксировали сверхсветовые скорости и в исследованиях космических лучей (потоков высокоэнергичных частиц). Бомбардируя ядра атомов земной атмосферы, они рождают ливни вторичных частиц, некоторые из которых, как оказалось, проходят путь до земных детекторов за время, много меньшее времени нужного для этого свету [15, с. 236]. Выходит, некоторые частицы, образующие ливни, летят со сверхсветовыми скоростями, если измерять их не косвенно, — по формулам СТО, а — непосредственно деля путь на время пути.
Впрочем, вопреки всем фактам, академическая наука не признаёт этих опытно доказанных результатов, объясняя их случайными ошибками эксперимента, — лишь потому, что они противоречат догме СТО. В этом "представители" науки полностью солидарны с Эйнштейном, который ни во что не ставил физический опыт (особенно если тот противоречил его теории относительности) и утверждал, что именно теория должна предписывать, какие факты можно наблюдать в опыте, а какие — нельзя. Такое самодурство академиков XX века, не признающих ни баллистической теории, ни падения из космоса сверхсветовых частиц, очень напоминает отрицание французскими академиками XVIII века болидов и засвидетельствованного падения с неба камней-метеоритов, тоже противоречивших догме. Подобные догматики, отрицающие очевидные факты, в итоге всегда становятся всеобщим посмешищем.
Ныне уже ряд фактов доказывает существование сверхсветовых частиц. В том числе, это и упомянутая способность некоторых короткоживущих частиц космических ливней достигать земной поверхности, что проще объяснить не продлением их жизни, а сверхсветовой скоростью. Да и огромные энергии Eчастиц космического излучения, происхождение которых нынешняя наука толком объяснить не может, говорят, согласно БТР и классической формуле E= mV 2/2, об их сверхсветовой скорости V. Такие скорости частицы могут набирать как раз в процессе распадов, особенно, — многоступенчатых. Словно у ракеты, отбрасывающей отработанные ступени, продукты деления частиц обретают, помимо скорости распада, скорость родительской частицы. Затем делятся продукты, что приводит к ещё большему разгону. Поэтому, когда появятся сверхсветовые связь и транспорт, они наверняка будут работать на микрочастицах (§ 5.10, § 5.11). Путь в космос пролегает через микромир! Не зря Циолковский, как изобретатель ракет, допускал полёты со сверхсветовыми скоростями и считал теорию относительности с растяжением времени абсурдом.
Скорости частиц космического излучения можно измерять двумя путями: по их энергии из формулы E=Mc 2с учётом релятивистской зависимости массы от скорости; или непосредственно, деля их путь сквозь атмосферу — на время пути. И, если первый метод, по определению, не может дать скорость больше скорости света, то в прямых измерениях у частиц не раз фиксировали скорость многократно превышающую световую. Аналогично в ускорителях-синхротронах скорость электронов можно искать по релятивистской формуле E=Mc 2, а можно — напрямую, умножив периметр π Dускорителя на частоту fускоряющего поля, равную частоте обращения частицы в ускорителе (Рис. 48). Диаметр Dмощных синхротронов — 100–200 метров, ускоряющее поле ВЧ-диапазона, то есть f=3–30 МГц. Отсюда скорость электронов V=π Df=10 9..10 10м/с, что в разы и десятки раз больше скорости света. Это вполне согласуется со скоростью, найденной из энергии Eэлектронов, по классической формуле E= MV 2/2. Уже для электронов с энергией в несколько МэВ скорость оказывается заметно выше, чем у света.
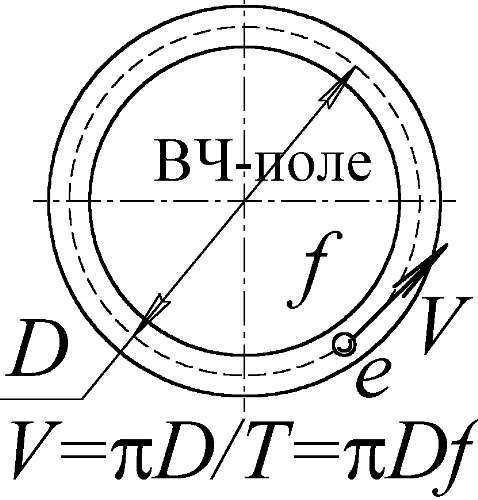
Рис. 48. Прямой расчёт скорости V электрона в синхротроне даёт V>c.
Однако, учёные, обнаружив это противоречие СТО, разрешили его чисто формально: ввели кратность ускорения q, то есть произвольно приняли, что частицы в ускорителе вращаются не с частотой ускоряющего поля, а с частотой в целое число qраз меньшей. Поэтому, вместо одного сгустка частиц в ускорителе вдоль кольца якобы возникает несколько сгустков — их число равно кратности ускорения, и частота ускоряющего поля будто бы совпадает именно с частотой прихода этих сгустков. Но, в таком случае, почему же не получается ускорять электроны до энергий в ГэВы, используя меньшие частоты ускоряющего поля? Почему для наиболее энергичных электронов всегда приходится вводить кратность ускорения q>1? Ответа нет. Точнее он есть, но приходится не по вкусу сторонникам СТО, ибо ответ в том, что высокоэнергичные электроны кружатся с частотой равной частоте ускоряющего поля и потому их скорости в десятки раз больше скорости света (подробное обоснование этого есть на сайте А. Мамаева: www.acmephysics.narod.ru).
Судя по всему, сверхсветовые частицы возникают не только в циклических, но и в линейных, а также плазменных ускорителях, где тоже достигнуты энергии электронов в десятки МэВ и даже ГэВы. В ряде таких устройств частицы разгоняются продольным полем электромагнитной волны, бегущей в полом волноводе или в плазме. Но фазовая скорость волн в гладких волноводах и плазме больше скорости света! Поэтому сверхсветовой скоростью должны обладать и частицы, подгоняемые, несомые этой волной. Ведь только при условии синхронизма (равенства скорости частиц и волны) ускоритель эффективен. Обычно утверждают, что в этих ускорителях волноводы снабжены диафрагмами, снижающими фазовую скорость в сравнении с гладкими волноводами, что якобы и обеспечивает движение волн и частиц с досветовой скоростью. Но где гарантия, что это снижение скорости столь значительно? Чтобы проверить это, надо непосредственно (пролётным методом) измерить скорость Vэлектронов и подгоняющих их волн. Это легко сделать по школьной формуле V=L/ T, деля путь частицы Lна время пролёта T, а в случае волны деля её длину L=λ (измеренную методом стоячих волн в волноводе) на период Tэлектрических колебаний. Вполне возможно, что эти прямые измерения выявят сверхсветовые скорости электронов, близкие к находимым по классической формуле E= mV 2/2, из их энергий в десятки и сотни МэВ. Ведь, даже при энергии Eэлектронов порядка 1 МэВ, их скорость Vдолжна превышать световую.