И всё же, как показал Ритц, все эти эксперименты можно объяснить классически, не прибегая к сомнительному эффекту изменения массы, и без отказа от привычного закона сохранения массы, — достаточно лишь учесть открытое в БТР влияние движения заряда на величину действующей на него электрической силы. Из таких экспериментов наиболее известен опыт Вальтера Кауфмана [55], где впервые обнаружился эффект увеличения массы электронов с ростом их скорости. Однако Ритц показал, что для объяснения эксперимента ни к чему считать массу переменной [8]. Напомним, что в опыте Кауфмана электрон "взвешивали", наблюдая, насколько тот отклонится, пролетев между пластинами конденсатора и полюсами магнита (Рис. 41). В самом деле, судя по тому, насколько электрон отклоняется электрическим и магнитным полем, из величины этих полей легко найти его массу. Ведь отклонения, измеренные по следу, оставляемому электронным пучком на люминесцентном экране, дают величину ускорения a, связанную по второму закону Ньютона a=F/mс массой mэлектрона. Но оказалось, что у электронов, летящих с разными скоростями, ускорения aразличны: они тем меньше, чем выше скорость. А, поскольку, следуя максвелловской электродинамике, считали, что сила F, действующая на электрон, не зависит от его скорости, пришли к абсурдному выводу, согласно которому по мере разгона электрона растёт его масса m. Но, ведь, куда естественней предположить, что масса постоянна, а изменяется сила F.
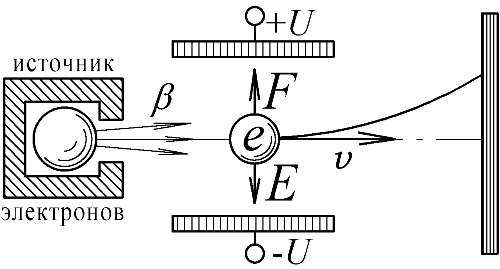
Рис. 41. Опыт Кауфмана — исследование отклонений быстро летящих электронов в электрических и магнитных полях.
Такое предположение тем более естественно, что, как выяснили ранее, скорость заряда и впрямь может влиять на величину электрической и магнитной силы (§ 1.7). Поэтому, согласно Ритцу, куда естественней считать, что электроны получают разные ускорения от разных сил, а не масс. Так, например, если пружинные весы показывают в зависимости от условий (скажем, от высоты или ускорения) разный вес гири, вряд ли мы сочтём, что меняется её масса. Скорее мы решим, что врут весы, и, в действительности, меняется сила тяжести и сила веса. То же — и в опытах по взвешиванию электрона электромагнитными весами, где влияние движения на величину кулоновской силы, в отличие от влияния на массу, кажется вполне возможным. В БТР зависимость силы от скорости — это обязательное следствие предложенной Ритцем модели взаимодействия зарядов. Ведь, если отталкивание зарядов создаётся ударами испускаемых ими со скоростью света частиц (реонов), то частицы эти не смогут догнать электрон, движущийся с той же скоростью c, а значит, не смогут ударно воздействовать на него. Вот и кажется, что масса электрона бесконечна, хотя реальная причина в нулевой силе. Такой мнимый бесконечный рост массы заряда с приближением его скорости к c, задолго до опыта Кауфмана предсказывал ещё В. Вебер на основе своей электродинамической теории, этого прообраза электродинамики В. Ритца [106].
Рассмотрим вопрос количественно. Теоретически, след электронного луча на экране должен был иметь форму параболы с уравнением
y=kx 2Em/H 2,
где k— некоторая постоянная, Eи H— напряжённости электрического и магнитного полей, а m— масса электрона. Наблюдаемая же кривая отличалась от этой параболы так, будто с ростом скорости масса mувеличивалась пропорционально (1+ v 2/2 c 2). Но ведь, как выяснено, почти так же, пропорционально (1+ v 2/3 c 2) нарастает со скоростью заряда электрическая сила и поле E. Учёт переменности Eпри постоянной массе внесёт в уравнение параболы почти те же изменения, что и учёт переменности mпри постоянном E. Разница же коэффициентов (в полтора раза) устраняется более точным расчётом, представленным в работе Ритца [8]. О причинах этого постоянного отличия в полтора раза в меньшую сторону было сказано выше (§ 1.7).
Итак, опыт Кауфмана продемонстрировал ошибочность прежней физики. Но, если Эйнштейн видел выход в отказе от классической механики, при сохранении электродинамики Максвелла (изменение массы при неизменной электрической силе), то Ритц счёл, что намного более естественно отказаться именно от электродинамики Максвелла, при сохранении классической механики (изменение электрической силы при неизменной массе электрона). Вывод Ритца тем более естественен, что именно отказ от максвелловской электродинамики и создание новой электродинамики БТР на базе классической механики, позволяет легко, без каких-либо формальных приёмов и произвольных подтасовок (имеющих место в СТО), получить правильный закон изменения электрической силы, объясняющий опыт Кауфмана.
В самом деле, эффект мнимого изменения массы легко может быть объяснён с помощью классической механики — даже на пальцах. Поскольку электрическое воздействие создаётся потоком реонов, то при движении электрона скорость реонов относительно него меняется. Реонам приходится догонять убегающий от них электрон, соответственно, сила и частота их ударов об электрон — снижается, а, потому, — уменьшается и вызываемое реонами электрическое воздействие на электрон. Таким образом, чем выше скорость электрона, тем меньше сила электрического воздействия на него, а, значит, меньше и вызываемое этой силой ускорение и отклонение электрона. Это уменьшение ускорения и объясняют увеличившейся массой, тогда как реальная причина — в уменьшении силы.
Эффект изменения массы наблюдался и для других частиц, например, при их разгоне в циклотроне. Оказалось, что циклотрон не может полностью реализовать своих возможностей и передать частицам свою максимальную мощность. Дело в том, что кружащиеся в циклотроне частицы, разгоняемые периодично меняющимся электрическим полем, с увеличением их энергии и скорости движения — за счёт изменения массы, а, значит, и частоты обращения, выходят из резонанса с колебаниями электрического поля. Поэтому, поле перестаёт передавать частицам энергию. Лишь изменяя частоту ускоряющего поля, как это делают в синхротронах, можно достичь максимальной эффективности ускорителя. И всё же по логике БТР, и в этом случае, нет, в действительности, никакого изменения массы. Ведь в ускорителе частота обращения заряженных частиц определяется их ускорением, то есть, опять же, — отношением силы (Лоренца) и массы. И опять причина изменения частоты обращения с ростом скорости состоит не в изменении массы, а в изменении вслед за скоростью — силы Лоренца. Сила Лоренца F=qVB, действительно, меняется вместе со скоростью Vчастицы. Это линейное изменение силы необходимо для обеспечения постоянства частоты ω= qB/m, крайне важного в циклотроне: F=qVB=ma=mVω. Однако, движение заряда вносит, как показал Ритц, ещё и нелинейные поправки в величину силы Лоренца, становящиеся заметными на больших скоростях. Из-за этого, с увеличением скорости заряда — уменьшается частота обращения ω= F/mV, что, однако, расценивают как увеличение массы m, хотя реально масса постоянна, а меняется сила.
Ещё задолго до Ритца учёные догадались, что электричество по-разному действует на движущийся и покоящийся заряды. На этом фундаменте, собственно говоря, и строилась прежняя электродинамика Вебера и Гаусса. С приходом полевой, эфирной электродинамики Максвелла от этой плодотворной идеи отказались. Когда же выяснилось, что эфир — это фикция, и, следовательно, основанная на нём максвеллова электродинамика ошибочна, учёные не захотели вернуться к прежним воззрениям на природу электричества, но предпочли согласовывать несогласуемое: максвеллову электродинамику и факт отсутствия эфира. Это и породило, по признанию Эйнштейна, его теорию относительности и все её парадоксы. Таким образом, отказ от теории относительности — невозможен без отказа от электродинамики Максвелла.