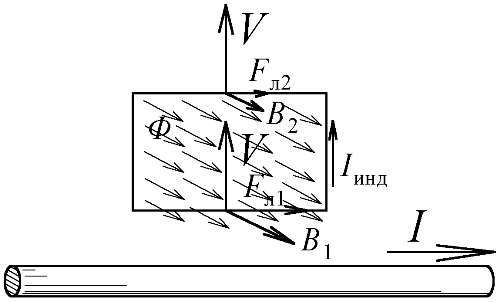
Рис. 18. Движение проволочной рамки ведёт к уменьшению потока Ф поля B через рамку и создаёт в ней силы Лоренца, наводящие ЭДС индукции с током I индв контуре.
Впрочем, и формула Вебера была эмпирической. Строго её обосновал Вальтер Ритц, получив формулу, как прямое следствие открытого им механизма взаимодействия элементарных зарядов (электронов) — посредством обмена стандартными микрочастицами (реонами). Именно так он вывел из своей модели силы магнитного взаимодействия (§ 1.7). В своём главном труде [8] Ритц объяснил не только все магнитные эффекты, но и явление электромагнитной индукции, открытое Фарадеем. Суть его в том, что изменение магнитного потока Фвектора Bчерез замкнутый контур (скажем, проволочное кольцо) наводит в этом контуре ЭДС индукции, создающей ток индукции и, по правилу Ленца, мешающей изменению потока [60].
Рассмотрим прямоугольную проволочную рамку и лежащий в её плоскости проводник с током (Рис. 18). По закону Фарадея, удаление рамки от провода со скоростью Vнаведёт в рамке ЭДС индукции U =-dФ/dt. Но и эта индукционная сила, по своей природе, — чисто электрическая, ибо, подобно магнитной силе, вызвана малым изменением электровзаимодействия зарядов от их движения. Как легко вычислить, ЭДС U =-dФ/dtсоздаётся разницей сил Лоренца F л1—F л2, действующих на заряды в ближнем и дальнем участке рамки, поскольку поле B 2меньше, чем в ближнем B 1[45]. В силу классического принципа относительности, то же получим и в случае, если рамка неподвижна, а удаляется проводник с током. Сложнее случай, когда провод и рамка неподвижны, но меняется ток в проводнике и создаваемое им магнитное поле Bи его поток Фчерез рамку (Рис. 19). В этом случае, из-за эффекта Ритца и запаздывания электрических воздействий разные участки рамки воспримут воздействие движущихся с ускорением aзарядов проводника с разным запозданием и интенсивностью. Это снова породит электрическую силу индукции U=-dФ/dtи ток в рамке.
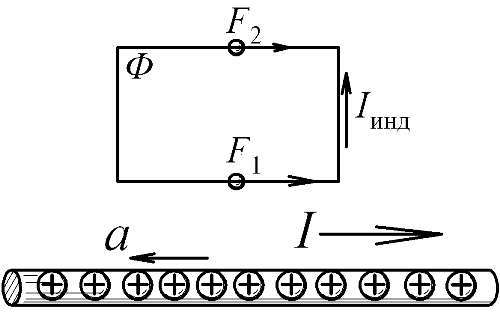
Рис. 19. Замедление зарядов в проводнике (ускорение a направлено против скорости) снижает величину тока I и вызванный им поток индукции Ф через рамку, а также создаёт разность сил, наводящих ЭДС и ток индукции в контуре.
Итак, магнитные, индукционные и прочие электродинамические эффекты, включая релятивистские, возникают в БТР как малые добавки к силе электрического воздействия от равномерного или ускоренного движения зарядов. Эти добавки возникают при учёте высших порядков при разложении электрической силы в ряд по степеням V/ cи Rа/c 2. Влиянию этих малых, но весьма существенных поправок Ритц придавал основное значение в своей электродинамике, показав, что эти добавки вызваны запаздыванием воздействий, конечной скоростью их распространения (см. эпиграф § 1.8), отчего меняется частота fприхода реонов к заряду, а значит сила воздействия на него. То есть, электродинамические эффекты — это прямое следствие квадратичного эффекта Доплера и Ритца — изменения частоты f = f 0[1–V 2/c 2+Rа/c 2]от движения источника (см. § 1.20 и § 1.10). Потому похожее выражение получается и для силы взаимодействия зарядов F=F 0[1–V 2/c 2+2Rа/c 2].Это, как и все электродинамические эффекты, — прямое следствие открытых Ритцем пространственно-временных соотношений и конечной скорости cреонов, то есть запаздывания электрических сигналов. Именно единая кинетическая природа эффектов Доплера и Ритца позволяет понять, почему изменение потока Фчерез контур как от скорости (Рис. 18), так и от ускорения зарядов (Рис. 19), порождает одинаковую ЭДС индукции, а также найти исключения из этого эмпирического правила Фарадея.
Электродинамику Максвелла предпочли исконной веберовской ещё и потому, что он рассматривал электромагнитные явления в средах, Вебер же говорил лишь о взаимодействии в пустоте. Вдобавок электродинамику сред проще изучать в рамках полевого, эфирного подхода, на языке физики сплошных сред, к которым относили эфир. Но, как показал Лоренц в своей электронной теории, все выводы электродинамики Максвелла для диэлектриков, металлов, преломляющих сред, получаются и в прежнем описании элементарных взаимодействий зарядов в вакууме. Надо лишь представить среду совокупностью зарядов (электронов и ионов), смещаемых и колеблемых под действием внешних источников, тем самым порождая вторичные воздействия и волны, которые налагаются на исходные и потому преобразуют их. Так что и здесь концепция Ритца — логичней максвелловой, вводящей для каждой среды свои свойства эфира. Впрочем, учёные во главе с Лоренцем пытались встроить электронную теорию, отрицающую особую роль среды, — в максвеллову, хотя куда естественней она вписывалась в электродинамику Вебера.
Объясняет Ритц и электромагнитные волны, давшие признание электродинамике Максвелла (§ 1.11). Как показал Ритц, электромагнитные волны получались и в электродинамике Вебера, причём много проще. Если Максвеллу требовались нескончаемые превращения электрического и магнитного поля для распространения волн, то в электродинамике Ритца световые колебания возникали как естественное следствие передачи переменных электрических воздействий с конечной скоростью потока частиц, равной скорости света c. Опыты Герца доказали реальность электромагнитных волн, электрическую природу света, но ничуть не подтвердили физической реальности поля или эфира и основанной на них теории Максвелла. Таким образом, электродинамика Ритца описывает те же самые эффекты, что и электродинамика Максвелла, в большинстве случаев естественно приводя к тем же результатам. И лишь в тонких и ещё неисследованных эффектах можно найти расхождение между этими электродинамическими теориями, что позволит однажды строго, на основании опытов, сделать выбор в пользу одной из теорий. Но уже сейчас в пользу БТР говорит то, что в электродинамике Ритца все явления трактуются чисто механически, наглядно. Существование магнитных и индукционных эффектов в БТР само собой вытекает из модели взаимодействия зарядов и не нуждается, в отличие от максвелловой теории, в принятии искусственных дополнительных гипотез об абстрактных электрических и магнитных полях.
Физики, однако, боготворят Максвелла и его уравнения. Восхищение уравнениями Максвелла доходит до того, что их обожествляют, словно в них заключена вся мудрость природы, и всё из них следует. А между тем эти уравнения построены чисто формально, как произвольные обобщения эмпирически открытых законов. Так, первое уравнение Максвелла rot H=∂ D/∂t+ jи четвёртое уравнение div B=0 — это всего лишь обобщения известных законов Био-Савара-Лапласа и Ампера, позволяющих найти величину магнитного поля проводника с током. Второе уравнение Максвелла rot E=-∂ B/∂t — это просто обобщённый закон электромагнитной индукции Фарадея [88]. Наконец, третье уравнение div D=ρ — это, опять же, не более чем обобщение закона Кулона, задающего электрическое поле Dзаряда, и теоремы Остроградского-Гаусса. Иногда утверждают, что Максвелл, кроме обобщения этих известных законов, сделал важное и даже гениальное добавление — открыл ток смещения (∂ D/∂t — плотность этого тока), который, как следует из первого уравнения, создаёт магнитное поле H, подобно току проводимости ( j— его плотность).
А на деле всё это следовало из тех же законов Био-Савара и Ампера. Рассмотрим первое уравнение в интегральной форме ∫ L H dl= d/dt∫ S D ds +I. Оно читается так: "циркуляция вектора Hпо замкнутому контуру Lравна изменению по времени потока вектора Dчерез поверхность S, ограниченную контуром L, плюс ток проводимости Iчерез эту поверхность". Возьмём контур Lв виде кольца, а на оси кольца, перпендикулярной его плоскости S, разместим элемент тока, не пересекающий эту плоскость, то есть, в уравнении I=0. Но согласно закону Био-Савара на кольце Lвсё равно индуцируется магнитное поле H, направленное вдоль линии контура L, то есть имеющее отличную от нуля циркуляцию. Потому Максвелл был вынужден добавить в правую часть уравнения ток смещения d/dt∫ S D ds, дабы учесть предсказанное законом Био-Савара и Ампера влияние элементов тока, не пересекающих площадку S. Ток — это движение зарядов, которое ведёт к изменению созданного зарядами потока поля Dчерез поверхность S: если элемент тока направлен к кольцу, то заряды приближаются и созданный ими поток Dнарастает, отчего и создаётся магнитное поле на контуре L. То есть максвеллов ток смещения — это не более чем удобный эквивалент токов проводимости, не пересекающих S, то есть напрямую неучтённых в его уравнении.