Это подтверждается и значениями энергии максимумов рассеяния в опыте Рамзауэра, которые близки к энергиям возбуждения указанных газов (Таблица 11: энергии возбуждения атомов по книге [91, с. 44]). Из-за того, что резонансный пик кривой рассеяния по разным причинам сильно размыт, минимум рассеяния может заметно отстоять от максимума, а энергия максимума — не точно совпадать с энергией возбуждения.
И вовсе не увеличением размеров атомов объясняется в опыте Рамзауэра уменьшение энергии E 1максимума рассеяния, а тем, что энергия возбуждения (и ионизации) постепенно убывает при переходе от гелия к ксенону. Если же размеры атомов, действительно, иногда оценивают по рассеянию и дифракции на них электронов, то, возможно, ошибочностью такой методики измерения и вызваны большие расхождения (иногда в 5 раз) значений атомных радиусов, найденных разными методами.
Итак, опыт Рамзауэра-Таунсенда не подтверждает волновых свойств электрона и должен быть исключён из соответствующих разделов учебников. Казалось бы, ничего страшного: просто в данном опыте проявляется, как и во многих других, не волновая, а только корпускулярная сторона двуликого электрона, зато в других дифракционных опытах волновые свойства этих, да и других частиц налицо. Но не всё так просто…
В опыте Рамзауэра, как и в опыте Франка-Герца, волновые свойства электрона, приводящие к уменьшению рассеяния, всё же должны проявляться, если и не при указанных, то при чуть меньших значениях энергий. Но в том-то и дело, что на зависимостях (Рис. 164 и Рис. 165), кроме обязательных колебаний рассеяния, связанных с возбуждением спектральных линий и ионизацией атомов, — больше нет никаких других. Получается, что опыт Рамзауэра не только не подтверждает волновой природы электрона, но даже опровергает её.
Вдобавок, ошибочная волновая трактовка опыта Рамзауэра, вошедшая в учебники, подрывает доверие к волновому объяснению и всех остальных опытов по интерференции или дифракции электронов и других частиц. Как увидим, все эти опыты можно объяснить рационально, без привлечения волновых свойств частиц. Выходит, реально нет никакого корпускулярно-волнового дуализма, и учёные ожидаемое — принимают за действительное. Просто результаты опытов по интерференции электронов, как и результаты опыта Рамзауэра, были настолько необычны, казались столь противоречащими классическим представлениям, что волновая природа электрона была в них признана безоговорочно, и не было попыток дать опытам альтернативное объяснение. А, между тем, видим, что такое объяснение может быть найдено, его следует поискать. Не зря, даже Эйнштейн и Планк, которых никто не обвинит в слепой приверженности классическим взглядам, работами которых и было положено начало квантовой физике, до конца своих дней отрицали квантовую механику и индетерминизм явлений микромира, утверждая, что невозможно для частицы быть одновременно волной, а для волны — частицей. И многие другие физики верили, что со временем в каждом из случаев выживет только одна модель, которая объяснит как волновые, так и корпускулярные свойства частиц или волн. Эту точку зрения самоотверженно защищал и А.Г. Столетов (§ 4.3).
§ 4.11 Волновые свойства частиц
Его богатое воображение, его оптимистическая готовность овладеть проблемой, не затруднённые слишком критическим подходом, были бы здесь весьма уместны.
Вальтер Ритц, подобно Шерлоку Холмсу, был непревзойдённым мастером по простому рациональному объяснению, на первый взгляд, сверхъестественных явлений и загадочных фактов, оказавшихся не по зубам представителям официальных структур. Так, Ритц классически объяснил результат опыта Майкельсона, спектры атомов, излучение чёрного тела. И, в объяснении волновых свойств частиц, пожалуй, именно Ритц, которому было многое по плечу, благодаря его оптимизму и смелому воображению, предложил бы разгадку. Однажды он уже сделал это, объяснив на базе корпускулярной теории истечения света и баллистического принципа волновые свойства света, переносимого частицами-реонами. Несомненно, Ритц предложил бы разумное наглядное классическое объяснение и волновым свойствам всех других частиц.
Так, волновые свойства были обнаружены не только у электронов, но и у других частиц, — нейтронов, атомов и молекул. Но, совершенно так же, как в случае реонов и электронов, эти опыты можно объяснить классически, не прибегая к гипотезе корпускулярно-волнового дуализма, а продолжая считать частицы простыми телами, корпускулами.
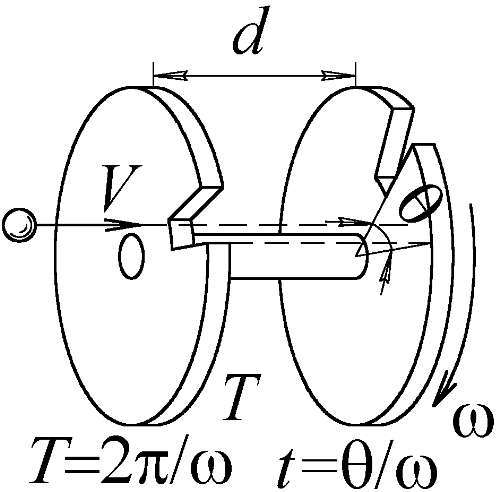
Рис. 166. Схема работы селектора скоростей, пропускающего молекулы со скоростями V=d/t.
Рассмотрим, например, дифракцию молекулярных пучков на поверхности кристалла. Сначала прибор, называемый "селектором скоростей" и представляющий собой два вращающихся диска с прорезями [134], выделяет из пучка частицы, обладающие заданной скоростью и соответствующей длиной волны де Бройля (Рис. 166). Этот пучок падает на кристалл и отражается, подобно электронному (Рис. 161). При этом, кроме пучка, отражённого под углом падения φ, возникают два побочных пучка, — два вторичных максимума, как от дифракции (Рис. 167). Эти максимумы отстоят от главного тем дальше, чем ниже скорость молекул и больше длина волны. Кажется, этот опыт уверенно доказывает волновые свойства частиц. Но это только кажется, поскольку он тоже имеет простую классическую трактовку. Прежде всего, селектор пропускает помимо молекул со скоростью V= d/t, частицы, летящие со скоростями d/( t+nT), где n —целое число, T— период обращения дисков. То есть, в кристалл попадают и сравнительно медленные частицы, за время пролёта которых селектор делает один или nоборотов.
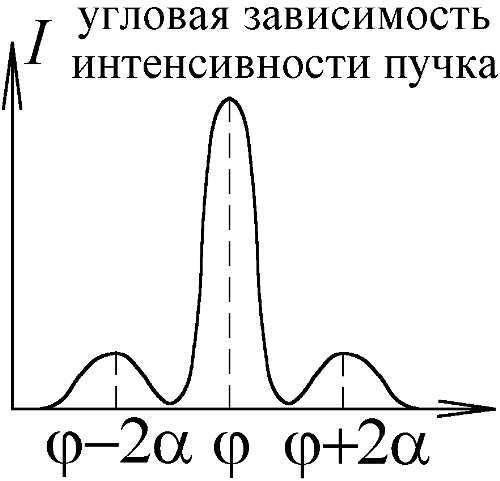
Рис. 167. Картина рассеяния пучка атомов кристаллом напоминает дифракционную, но объясняется классически.
Теперь рассмотрим частицу, падающую на поверхность кристалла. Атом отскакивает не от отдельных атомов кристалла, а от взаимодействия с их общим электрическим полем. Поле атомной плоскости имеет волнистые эквипотенциальные поверхности, горбы которых расположены напротив атомов, а впадины — между ними. При этом, чем дальше от границы кристалла, тем более плоскими и гладкими становятся плоскости равного потенциала. От этих эквипотенциальных поверхностей и отскакивают, отражаются атомы или молекулы газа. Чем выше энергия частиц газа, тем от более глубокой поверхности они отразятся, словно от жёсткой, то есть, — под углом равным углу падения. Если сечение поверхности изобразить синусоидой с предельной крутизной α, то видно, что атомы будут отражаться под любыми углами, заключёнными в пределах от φ–2α до φ+2α. Причём интенсивней всего идёт отражение именно под этими крайними углами: каждый пучок создаёт по два максимума (Рис. 168). У медленных частиц они отстоят мало, поскольку частицы отражаются внешними эквипотенциальными слоями, почти плоскими, — с малым α. Эти медленные молекулы с V= d/( t+nT), которых в газе больше всего, и создают высокий главный пик возле угла φ — максимумы слиты в один (Рис. 167). Зато быстрые молекулы c V= d/tдоходят до более глубоких слоёв с большей волнистостью и крутизной α. Именно они создают возле главного два побочных максимума, ошибочно принятых за дифракционные.
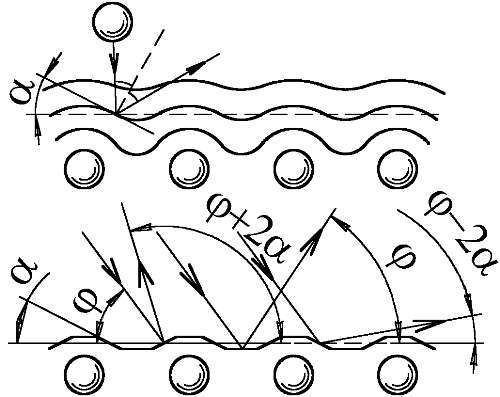
Рис. 168. Рассеяние атомов поверхностью кристалла под избранными углами — результат отражения атомов эквипотенциальными поверхностями.