Итак, опыт убеждает, что все так называемые "квантовые закономерности", открытые в явлениях фотоэффекта, фотоионизации и рождения электрон-позитронных пар, обусловлены отнюдь не свойствами света, но — свойствами атомов, вещества. Так, селективный и нелинейный фотоэффекты явно свидетельствуют, что процессы излучения и поглощения веществом света имеют резонансный, колебательный, волновой характер, а никак не квантовый. Лишь классическая модель фотоэффекта, которую отстаивал и отец фотоэффекта А. Столетов, способна помочь адекватному и простому пониманию всех закономерностей фотоэффекта.
§ 4.7 Эффект Комптона
Явление изменения длины волны при рассеянии света можно было бы объяснить с волновой точки зрения при помощи явления Доплера: электроны, рассеивающие рентгеновские лучи, под действием их выбрасываются из атомов по различным направлениям с разными скоростями. Таким образом, рассеянное излучение должно иметь изменённую длину волны в зависимости от скорости и направления движения рассеивающих электронов. Вычислив, как должны были бы двигаться рассеивающие электроны, нетрудно получить классическую картину явления Комптона.
Не составит большого труда объяснить с классических позиций и другое "квантовое" явление — эффект Комптона, который вместе с фотоэффектом считают неопровержимым доказательством фотонной теории. Суть его в том, что рентгеновские лучи претерпевают на электронах так называемое "комптоновское рассеяние" (Рис. 157). Причём, в отличие от обычного рассеяния, длины волн падающего λ 0и рассеянного λ' излучения не совпадают, а их разница жёстко связана с углом рассеяния θ соотношением
λ'—λ 0= 2λ кsin 2(θ/2),
где λ к— комптоновская длина, составляющая для электрона массы mвеличину λ к= h/mc= 2,4·10 –12м [134]. Кроме того, как показали опыты, электрон в процессе рассеяния испытывает отдачу, приобретая скорость, направленную под таким углом φ к падающему лучу, что tgφ= ctg(θ/2)/(1+λ к/λ 0). Всё выглядит так, словно не волна рассеивается на электроне, а с ним упруго сталкивается частица, фотон, передающий электрону часть своего импульса и энергии. К тому же, как утверждают многие учебники, классическое взаимодействие волны с электронами вещества не могло бы породить рассеянного излучения на смещённой частоте. Ведь свободный электрон, по теории Дж. Томсона, должен колебаться под действием электромагнитной волны — с частотой поля этой волны, а, значит, и излучение испускать — на той же частоте и с той же длиной волны λ 0[82]. А, между тем, рассеянное излучение в эффекте Комптона, кроме несмещённой компоненты спектра λ 0, содержит сдвинутую, — с длиной волны λ'.
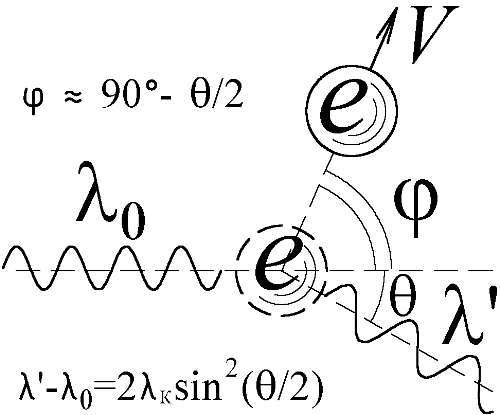
Рис. 157. Эффект Комптона.
Кроме того, совсем как в фотоэффекте, в комптоновском — скорость и энергия электрона часто превосходят те, которые ему могла бы сообщить волна в момент облучения [134]. Это, опять же, трактуют как соударение с электронами световой волны, собранной в порции, кванты. Но, в действительности, похоже, и здесь луч не отдаёт электронам энергию, а лишь высвобождает электроны, изначально обладавшие скоростью в атомах. Поэтому, никто ещё не смог наблюдать комптоновское рассеяние на свободных электронах. Учёные признают, что его дают только электроны атомов, но полагают, что атом, испустивший электрон, — это лишь досадная помеха и электроны в нём можно рассматривать как свободные. На самом же деле, без участия атомов комптон-эффект был бы вовсе невозможен, его никто и никогда не сможет наблюдать у свободных электронов. Так, в случае обратного комптон-эффекта, когда уже действительно свободно летящий электрон не поглощает, а, напротив, отдаёт энергию свету, имеет место лишь классическое рассеяние [151, с. 312]. Далее покажем, что и прямое комптоновское рассеяние имеет чисто классические причины.
Собственно говоря, некоторые учёные даже проговорились, что такое объяснение существовало, но было основательно забыто. Так, Г.С. Ландсберг пишет, вопреки часто приводимому в учебниках утверждению, по которому классическая теория не способна объяснить рассеяния на новой частоте, что реально и классика предсказывает смещённые компоненты излучения. Ведь, если учесть, что электроны, вылетающие из атомов под действием внутреннего фотоэффекта, обладают большими скоростями, то рассеянное ими излучение, по эффекту Доплера, обязано иметь иную длину волны [74]. Эта длина волны λ', в полном согласии с комптон-эффектом, будет зависеть от длины волны λ 0падающего излучения, от угла вылета электрона и направления рассеянного излучения. Так возникает классическая картина эффекта Комптона. Ландсберг не раскрывает подробностей этого описания и того, кто его автор. Поэтому попробуем реконструировать, восстановить эту забытую трактовку, отреставрировав классическую картину явления.
Пусть электромагнитная волна частоты f 0, падая на атом, "вырывает" из него электрон, имеющий, как показывает фотоэффект (§ 4.3), энергию mV 2/2= hf 0. Угол φ вылета электрона может оказаться любым. Падающая волна заставит этот свободно летящий со скоростью Vэлектрон колебаться, но, в силу эффекта Доплера, — с частотой f= f 0(1+ Vcosφ/ c), отличной от f 0(Рис. 158). Вибрирующий электрон излучает вторичные волны, частота прихода f'которых, в некотором направлении θ,— отлична от частоты их испускания f. Из эффекта Доплера f'= f(1+ Vcos(φ+θ)/ c)= f 0(1+ Vcosφ/ c)(1+ Vcos(φ+θ)/ c). Кроме того, падающая волна заставит колебаться и излучать с частотой f 0электроны, оставшиеся в атоме. Эти две волны от атома и свободного электрона интерферируют, но правильно сложиться не могут, поскольку их частоты f 0и f'не совпадают. Во всех направлениях эти две волны сложатся беспорядочно, создавая биения, или вообще не сложатся от несинхронного прихода. И, лишь в направлении θ, для которого f 0= f'= f 0(1+ Vcosφ/ c)(1+ Vcos(φ+θ)/ c), волны интерферируют за счёт равенства частот и одновременного прибытия, откуда cosφ= —cos(φ+θ), то есть φ=90°-θ/2.
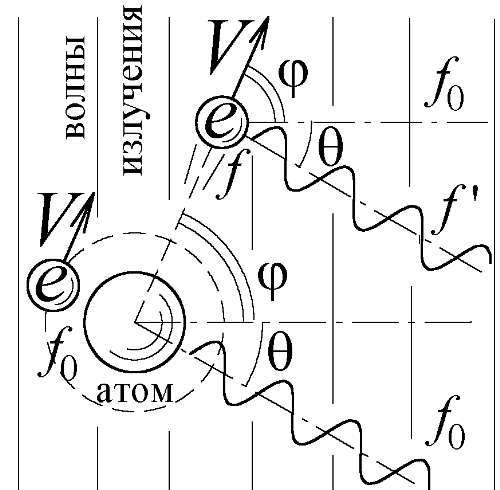
Рис. 158. Механизм комптон-эффекта: излучение f 0, "вырывая" электрон из атома, рассеивается им с частотой f'.
Подставляя значение φ, найдём, что лучи, идущие в направлении θ, имеют частоту
f'= f 0(1– Vsin(θ/2)/ c)(1+ Vsin(θ/2)/ c)= f 0(1–sin 2(θ/2) V 2/ c 2)
и длину волны
λ'= с/ f'= λ 0+ λ 0sin 2(θ/2) V 2/ c 2.
Учтя же, что для излучения, выбившего электрон, λ 0= c/ f 0=2 hc/ mV 2, найдём
λ'= λ 0+ sin 2(θ/2)2 h/ mc.
То есть, пришли к проверенной опытом формуле λ'—λ 0= 2λ кsin 2(θ/2), где λ к= h/mc. Также приходим к правильному соотношению углов рассеяния и отдачи, ибо если φ =90°- θ/2, то tgφ = ctg(θ/2). Это довольно точно совпадает с опытно проверенной зависимостью tgφ = ctg(θ/2)/(1+λ к/λ 0), поскольку λ к= 2,4·10 –12м обычно много меньше длины волны λ 0рентгеновского излучения, диапазон которого простирается от 10 –7до 10 –12метра. Лишь для самых жёстких рентгеновских лучей величина (1+λ к/λ 0) будет заметно отличаться от единицы. Но тогда надо, соответственно, уточнить и наш приближённый расчёт, ибо при сопоставимости λ к= h/mcи λ 0=2 ch/ mV 2скорость Vэлектрона становится сравнимой со скоростью света c, и в выражении для f'надо учесть квадратичный эффект Доплера (§ 1.20). При расчёте сделан и ряд других упрощений, конечно, не меняющих сути дела, поскольку более строгий классический анализ, учитывающий отдачу атома при испускании электрона, взаимодействие с волной обратного рассеяния и условие волнового синхронизма, даёт ту же картину эффекта Комптона.