Некоторые математики полагают, что математика автономна (гл. XIV), т.е. что ее аксиомы рождены чистым разумом или подсказаны опытом, а вся остальная математика построена на них уже независимо от опыта. Если встать на эту точку зрения, то как объяснить, почему математика применима к реальному миру, и особенно к физическим явлениям. На этот вопрос существует несколько ответов. Один из них состоит в том, что в математические аксиомы входят неопределяемые понятия, и, по-разному интерпретируя эти понятия, можно достичь согласия о описываемой физической ситуацией. Так, например, эллиптическая неевклидова геометрия применима и к обычным прямым на эллиптическойплоскости, под которой можно — понимать и обычные «физические» плоскости (ведь «в пределе» при очень большой длине каждой прямой эллиптическая геометрия переходит в евклидову!), и к геометрии на сфере, где «прямыми» служат дуги больших окружностей сферы, высекаемых из нее плоскостями, проходящими через центр сферы.
Объяснение такого рода предложил Пуанкаре. Ему хотелось, чтобы математика была чисто дедуктивной наукой, которая лишь шаг за шагом выводит следствия из исходных аксиом. Используя правдоподобные аксиомы, возможно подсказанные его чувственными восприятиями, человек создает евклидову или неевклидову геометрии. Аксиомы и теоремы этих геометрий не являются ни эмпирическими, ни априорными истинами. Они истинны или ложны ничуть не больше, чем правильно или неправильно использование полярных координат по сравнению с прямоугольными. Пуанкаре назвал эти геометрии соглашениями для упорядочения и измерения тел или замаскированными определениями понятий. Мы используем ту геометрию, которая наиболее удобна. Тем не менее, подчеркивал Пуанкаре, мы всегда используем евклидову геометрию c прямыми, понимаемыми в обычном смысле, т.е. как натянутые нити или край линейки, потому что евклидова геометрия самая простая. Почему же теоремы геометрии должны быть применимы к физическому миру? Ответ, данный Пуанкаре, гласил: потому что мы изменяем физические законы, стремясь привести их в соответствие с математикой, «подогнать» под нее.
Чтобы проиллюстрировать выдвинутый Пуанкаре тезис, рассмотрим, как геодезисты определяют расстояния. Сначала они выбирают удобный базис — отрезок AB(рис. 15.1), длина которого измеряется мерной лентой. Чтобы определить расстояние AC,геодезист измеряет угол CAB,визируя в специальную трубу, установленную в точке A,направление на точку C,а затем наводя трубу на точку B.По лимбу на теодолите геодезист узнает, на какой угол была повернута труба, и тем самым измеряет угол CAB.Аналогичным образом геодезист измеряет угол ABC.Предполагается, что лучи света, идущие из Cв Aи из Bв A,совпадают с отрезками прямых (натянутыми нитями), соединяющими точки Cи Bс точкой A.
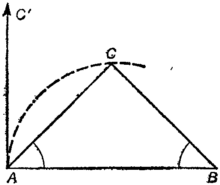
Рис 15.1.Измерение расстояний методом триангуляции.
Но мы знаем, что аксиомы евклидовой геометрии согласуются с представлением о прямой как о натянутой нити, поэтому геодезист при вычислении расстояний ACи BCсмело использует евклидову геометрию. Предположим теперь, что полученные геодезистом расстояния все же оказались неверными. Как это могло произойти? Луч света, идущий из точки Cв точку A,мог распространяться по траектории, показанной на рис. 15.1 пунктиром; при этом, чтобы поймать световой «зайчик», геодезисту приходилось наводить теодолит в точке Aпо касательной к описываемой лучом света траектории. Следовательно, теодолит мог быть наведен на точку C',хотя геодезист видел точку C,и вместо угла CABон измерил угол C'AB.В этом случае применение евклидовой геометрии могло бы дать неверные значения расстояний ACи BC.
Итак, возникает вопрос: по какому пути распространяются лучи света? Иногда они распространяются по «настоящим» (обычным) прямым, иногда изгибаются вследствие рефракции в атмосфере. Предположим, что геодезист определил расстояния ACи BCневерно. Не имея никаких оснований считать лучи света искривленными, он тем не менее счел их таковыми и в своих вычислениях обращался с отрезками ACи BCкак с криволинейными. Введя надлежащие поправки в измерения углов в пунктах Aи B,геодезист мог бы воспользоваться евклидовой геометрией и получить правильные значения расстояний ACи BC.
Приведем еще один пример, поясняющий тезис Пуанкаре о том, что математику можно подогнать под физическую реальность; этот пример касается вращения Земли. По мнению Пуанкаре, вращение Земли необходимо принять как физический факт, так как в астрономии это допущение приводит к более простой математической теории рассматриваемых явлений. Действительно, простота математической теории была единственным аргументом, который Коперник и Кеплер смогли привести в пользу гелиоцентрической системы по сравнению со старой геоцентрической системой Птолемея.
Развитая Пуанкаре философия науки обладает несомненным достоинством. Мы действительно пытаемся обходиться возможно более простой математикой и изменять в случае необходимости физические законы так, чтобы наши умозаключения находились в согласии с физическими фактами. Но современные физики и математики используют в качестве критерия простоту математической и физической теории в целом.И если для получения простейшей комбинированной [физико-математической] теории нам придется воспользоваться неевклидовой геометрией, как это сделал Эйнштейн в своей теории относительности {180}, то мы пойдем на это.
Хотя объяснение эффективности математики, предложенное Пуанкаре, было более подробным, в определенных пределах он считал верным и кантовское объяснение, а именно ту его часть, где говорится, что согласие между математикой и природой создается человеческим разумом. Так, в «Ценности науки» Пуанкаре утверждает:
Но та гармония, которую человеческий разум полагает открыть в природе, существует ли она вне человеческого разума? Без сомнения — нет; невозможна реальность, которая была бы полностью независима от ума, постигающего ее, видящего, чувствующего ее. Такой внешний мир, если бы даже он и существовал, никогда не был бы нам доступен. Но то, что мы называем объективной реальностью, в конечном счете есть то, что общо нескольким мыслящим существам и могло бы быть общо всем. Этой общей стороной, как мы увидим, может быть только гармония, выражающаяся математическими законами.
Есть и другое, несколько туманное, возможно, чрезмерно упрощенное объяснение эффективности математики. Согласно этому объяснению, существует объективный физический мир и человек стремится согласовать с ним свою математику. Мы вносим необходимые коррективы, когда приложения обнаруживают неточности математического описания или прямые ошибки в нашей математике. Подобную точку зрения Гильберт высказал в докладе на II Международном математическом конгрессе в 1900 г.:
А между тем во время действия созидательной силы чистого мышления внешний мир снова настаивает на своих правах: он навязывает нам своими реальными фактами новые вопросы и открывает нам новые области математического знания. И в процессе включения этих новых областей знания в царство чистой мысли мы часто находим ответы на старые нерешенные проблемы и таким путем наилучшим образом продвигаем вперед новые теории. На этой постоянно повторяющейся и сменяющейся игре между мышлением и опытом, мне кажется, и основаны те многочисленные и поражающие аналогии и та кажущаяся предустановленной гармония, которые математик так часто обнаруживает в задачах, методах и понятиях различных областей знания.
180
Здесь имеются в виду описывающая пространство-время специальной теории относительности (СТО) так называемая псевдоевклидова геометрия Минковского(см. по этому поводу, например, классическую книгу [127]) и риманова(точнее, псевдориманова) геометрия,являющаяся базисом общей теории относительности (см., скажем, основополагающую статью [128] или ту же книгу [127]).