Лит.: Пеев П., Мулешков С., Маринов Х., София, София, 1965; София. [Альбом. Сост. С. Кожухаров], София, 1969; Ташев П., София. Архитектурно-градоустройственно развитие, София, 1972.

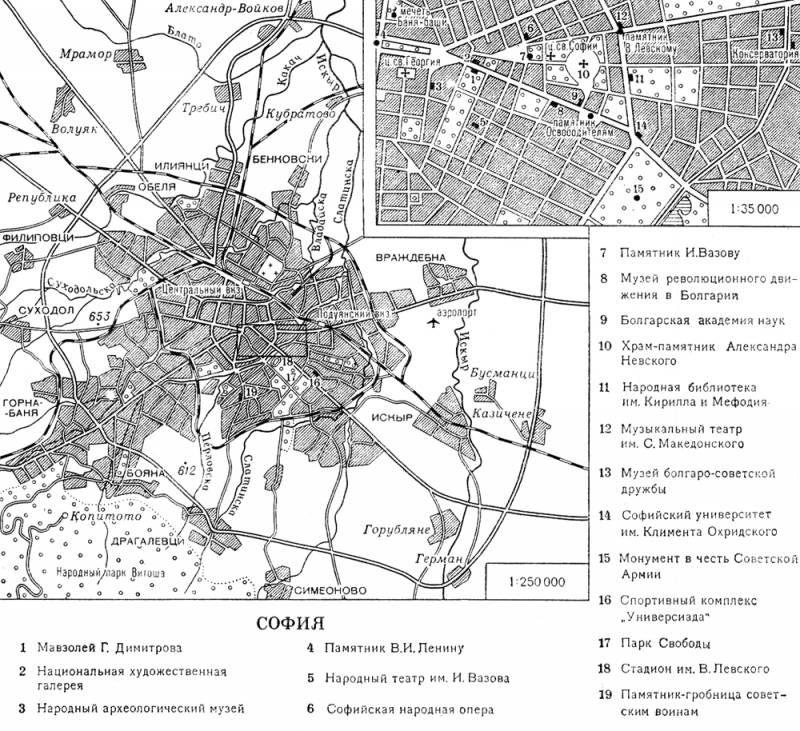
София. План города.

Жилищный комплекс Восток. 1970—73. Архитектор С. Георгиева.

Академия наук. 1892. Архитектор М. Майер.

Дом партии. 1952—55. Архитекторы П. Златев и др.

Монумент в честь Советской Армии в Софии. 1954. Архитекторы Д. Митов и Л. Нейков, скульптуры И. Фунев, Л. Далчев, И. Лазаров и др.

Болгария. Церковь св. Софии в г. София. 5—6 вв.

Университет им. Климента Охридского. 1924—34. Архитектор Й. Миланов.

Спортивный зал «Универсиада». 1961. Архитекторы А. Баров и др.

Церковь св. Георгия (в 3—-4 вв. перестроена из древнеримского сооружения).

Болгария. Ф. Фельнер, Г. Хельмер. Народный театр им. И. Вазова в Софии. 1904.

Болгария. София. В центре — собор Александра Невского.

Национальная художественная галерея (б. царский дворец). Перестроена в 1877—87. Архитектор П. Момчилов.

Софокл

Софо'кл (Sophokles) (около 496—406 до н. э.). Древнегреческий драматург. Родился в предместье Афин — Колоне. Избирался на важные государственные должности, был близок к кругу Перикла. По античным свидетельствам, написал свыше 120 драм; первую победу на состязаниях трагических поэтов одержал в 468. Целиком дошли до нас трагедии «Аякс» (до 442), «Антигона» (около 441), «Царь Эдип» (около 425), «Филоктет» (409), «Трахинянки» и «Электра» (даты обеих неизвестны), «Эдип в Колоне» (поставлена в 401). От прочих произведений сохранилось много фрагментов.

  Мировоззрение С. отражает сложность и противоречивость афинской демократии периода её высшего расцвета. С одной стороны, демократическая идеология, выросшая на основе «... совместной частной собственности активных граждан государства...» (Маркс К. и Энгельс Ф., Соч., 2 изд., т. 3, с. 21), видела свой оплот во всевластии божественного промысла, в незыблемости традиционных установлений; с другой стороны — в условиях наиболее свободного для того времени развития личности всё настойчивее становилась тенденция к её высвобождению из полисных связей. Испытания, выпадающие на долю человека, не могли найти удовлетворительного объяснения в божественной воле, и С., озабоченный сохранением полисного единства, не пытался обосновать божественное управление миром какими-либо этическими соображениями. В то же время его привлекал активный, отвечающий за свои решения человек. В «Аяксе» герой осознаёт несовместимость содеянного им с нравственным кодексом доблестного вождя и в добровольной смерти находит освобождение от позора и бесчестья. В «Царе Эдипе» непреклонное расследование героем тайны своего рождения и прошлого возлагает на него объективную ответственность за невольные преступления, хотя и не даёт основания толковать трагедию в категориях субъективной вины и божественного возмездия. Цельным, неколебимым в своём решении человеком предстаёт Антигона с её героической защитой «неписаных» законов от произвола отдельной личности, прикрывающейся авторитетом государства. Герои С. свободны от всего второстепенного и слишком личного, в них сильно идеальное начало. Введение третьего актёра позволило С. усилить напряжение в развитии действия, обогатить изображение вовлечённых в него лиц. Несмотря на увеличившийся состав хора (15 человек), объём и значение хоровых партий в трагедиях С. существенно сократились по сравнению с произведениями Эсхила.

  Сюжеты и образы С. использовались как в последующей античной (Акций, Сенека), так и в новой европейской литературе от эпохи классицизма (Ж. Ротру, П. Корнель) вплоть до 20 в. (Ж. Жироду, Ж. Ануй, Б. Брехт и др.). Глубокий интерес к творчеству С. проявлялся в исследованиях и высказываниях по теории трагедии (Г. Э. Лессинг, И. В. Гёте, братья Шлегель, Ф. Шиллер, В. Г. Белинский). С середины 19 в. трагедии С. ставятся в театрах всего мира.

  Соч.: Sophocle, Tragédies, t. 1—3, P., 1955—60: в рус. пер. — Драмы. Пер. Ф. Зелинского, т. 1—3, М., 1914—15; Трагедии. Пер. С. Шервинского, М., 1958.

  Лит.: Радциг С. И., К вопросу о мировоззрении Софокла, «Вестник древней истории». 1957, № 4; Lesky A., Die tragische Dichtung der Hellenen, 3 Aufl., Gott., 1972, S. 169—274.

  В. Н. Ярхо.

Софокусные кривые

Софо'кусные кривы'е, конфокальные кривые [от лат. con (cum) — с, вместе и фокус], линии второго порядка, имеющие общие фокусы. Если F и F'— две данные точки плоскости, то через каждую точку плоскости проходит один эллипс и одна гипербола, имеющие F и F' своими фокусами (рис. 1).

  Каждый эллипс ортогонален любой софокусной с ним гиперболе, т. е. пересекается с ней (в четырёх точках) под прямым углом (углом между двумя кривыми в точке пересечения называется угол между их касательными). Всё множество софокусных эллипсов и гипербол в надлежащей системе координат определяется уравнением

 (*)

где с — расстояние фокусов от начала координат, а l — переменный параметр. При l > с² это уравнение определяет эллипс, при 0< l< с² — гиперболу (при l < 0 — мнимую линию 2-го порядка). Если один из фокусов стремится к бесконечности, то в пределе получаются два семейства софокусных парабол (рис. 2); любые две параболы, относящиеся к разным семействам, также ортогональны друг другу. При помощи софокусных эллипсов и гипербол на плоскости вводится система т. н. эллиптических координат. Именно, если М (х, у) — произвольная точка плоскости, то, подставляя ее координаты х и у в уравнение (*), получим квадратное уравнение для l; корни его l₁, l₂ называются эллиптическими координатами точки М. Сами софокусные эллипсы и гиперболы составляют координатную сеть эллиптической координатной системы, т. с. определяются уравнениями l = const. l₂ = const.

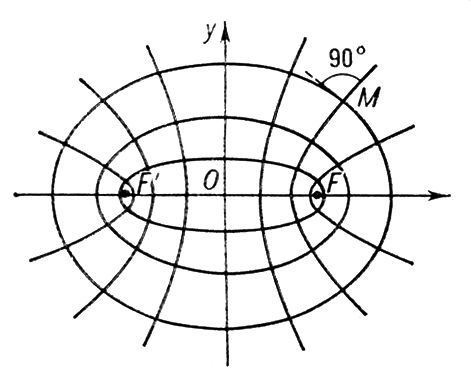
Рис. 1 к ст. Софокусные кривые.

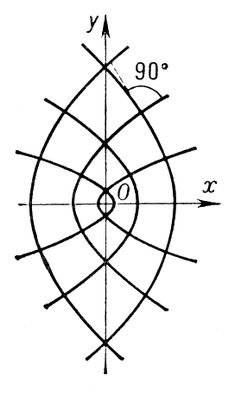
Рис. 2 к ст. Софокусные кривые.