На молекулярном уровне по принципу О. с. регулируется огромное число ферментативных реакций, одновременно протекающих в живой клетке. Координация этой сложной взаимосвязанной системы осуществляется путём изменения активности ферментов (отрицательную О. с. осуществляют ингибиторы, положительную — стимуляторы) или скорости их синтеза (О. с. осуществляют эффекторы; см. Оперон).

  Комбинации положительных и отрицательных О. с. обусловливают альтернативную смену физиологических состояний (например, сон — бодрствование). Изучение кривой развития патологических процессов неинфекционного характера (трофические язвы, гипертония, маниакально-депрессивный психоз, эпилепсия и т.д.) позволяет, исходя из результата, определить наиболее вероятный тип О. с., лежащий в основе заболевания, и ограничить изучение его этиологии и патогенеза механизмами определённой категории. Живые объекты как наиболее совершенные саморегулирующиеся системы богаты различными типами О. с.; изучение последних — весьма продуктивно для исследования биологических явлений и установления их специфичности.

  Лит.: Малиновский А. А., Типы управляющих биологических систем и их приспособительное значение, в сборнике: Проблемы кибернетики, № 4, М., 1961, с. 151—181; Регуляторные механизмы клетки, пер. с англ., М., 1964; Петрушенко Л.А., Принцип обратной связи, М., 1967: Винер Н., Кибернетика или управление и связь в животном и машине, пер. с англ., М., 1968; Шмальгаузен И. И., Кибернетические вопросы биологии, Новосибирск, 1968.

  А. А. Малиновский.

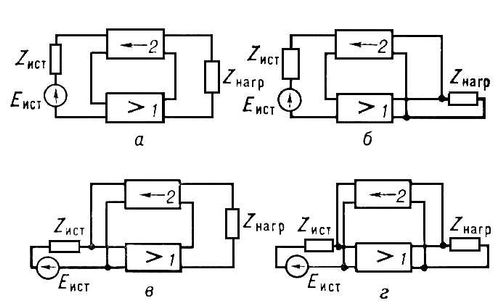
Рис. 1. Схемы усилителей с различными видами цепей обратной связи: а — последовательная обратная связь по току; б — последовательная обратная связь по напряжению; в — параллельная обратная связь по току; г — параллельная обратная связь по напряжению. 1 — усилитель электрических колебаний; 2 — цепь обратной связи (стрелкой показано направление распространения сигнала по цепи обратной связи от её входных зажимов к выходным): Z_ист — полное сопротивление источника сигнала Е_ист; Z_нагр — полное нагрузочное сопротивление усилителя.

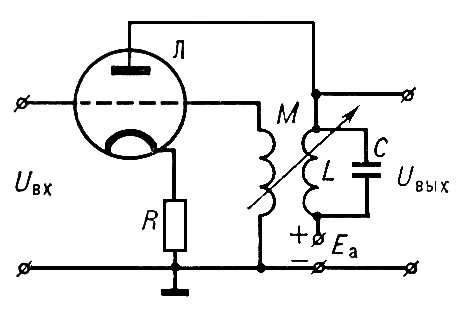
Рис. 2. Ламповый усилитель электрических колебаний с обратной связью: U_вх — напряжение на входе усилителя; Л — электронная лампа; R — резистор в цепи катода лампы; L и С — соответственно индуктивность и ёмкость колебательного контура в цепи анода лампы; М — взаимная индуктивность, связывающая цепи анода и управляющей сетки лампы; U_вых — напряжение на выходе усилителя; E_a — напряжение анодного питания.

Обратная сила закона

Обра'тная си'ла зако'на, распространение действия закона на отношения, возникшие до его издания. Как правило, закон обратной силы не имеет, т. е. он применяется только к отношениям, правам и обязанностям, которые возникли после вступления данного закона в силу. Это вносит определённость и устойчивость в общественную жизнь, в осуществление правовых предписаний, создаёт у граждан уверенность в незыблемости их прав и обязанностей, предусмотренных действующими законами. При необходимости законодатель может специальным указанием придать тому или иному закону (иногда некоторым статьям закона) обратную силу, т. е. распространить вновь принятый закон на отношения, которые возникли ранее. В СССР обратная сила придаётся также уголовным законам, устраняющим наказуемость деяния или смягчающим меру наказания. В этом проявляется гуманизм советского права, исходящего из нецелесообразности наказывать вообще (или наказывать столь же строго) за действие, которое ранее считалось преступлением, а к моменту выхода нового закона потеряло прежний социально опасный характер. Наряду с принципом О. с. з. (т. н. ретроактивность) возможно также «переживание старого закона», т. е. распространение действия закона, потерявшего силу, на отношения, имеющие место после его отмены (т. н. ультраактивность).

Обратная теорема

Обра'тная теоре'ма, теорема, условием которой служит заключение исходной (прямой) теоремы, а заключением — условие. Обратной к О. т. будет исходная (прямая) теорема. Таким образом, прямая и О. т. взаимно обратны. Например, теоремы: «если два угла треугольника равны, то их биссектрисы равны» и «если две биссектрисы треугольника равны, то соответствующие им углы равны» — являются обратными друг другу. Из справедливости какой-нибудь теоремы, вообще говоря, не следует справедливость обратной к ней теоремы. Например, теорема: «если число делится на 6, то оно делится на 3» — верна, а О. т.: «если число делится на 3, то оно делится на 6» — неверна. Даже если О. т. верна, для её доказательства могут оказаться недостаточными средства, используемые при доказательстве прямой теоремы. Например, в евклидовой геометрии верны как теорема «две прямые на плоскости, имеющие общий перпендикуляр, не пересекаются», так и обратная к ней теорема «две непересекающиеся прямые на плоскости имеют общий перпендикуляр». Однако вторая (обратная) теорема основывается на евклидовой аксиоме параллельных, тогда как для доказательства первой эта аксиома не нужна. В Лобачевского геометрии вторая просто неверна, тогда как первая остаётся в силе. О. т. равносильна теореме, противоположной к прямой, т. е. теореме, в которой условие и заключение прямой теоремы заменены их отрицаниями. Поэтому прямая теорема равносильна теореме, противоположной к обратной, т. е. теореме, утверждающей, что если неверно заключение прямой теоремы, то неверно и её условие. Известный способ «доказательства от противного» как раз и представляет собой замену доказательства прямой теоремы доказательством теоремы, противоположной к обратной. Справедливость обеих взаимно обратных теорем означает, что выполнение условия любой из них не только достаточно, но и необходимо для справедливости заключения (см. Необходимые и достаточные условия).

Обратная функция

Обра'тная фу'нкция, функция, обращающая зависимость, выражаемую данной функцией. Так, если у = f (x) — данная функция, то переменная х, рассматриваемая как функция переменной у, х = j (y), является обратной по отношению к данной функции у = f (x). Например, О. ф. для у = ax + b (а¹0) является х = (у—b)/a, О. ф. для у = е^х является х = ln у и т.д. Если х = j(y) есть О. ф. по отношению к у = f (x), то и у = f (x) есть О. ф. по отношению к х = j(y). Областью определения О. ф. является область значений данной функции, а областью значений О. ф.— область определения данной. Графики двух взаимно обратных функций у = f (x) и у = j (x) (где независимое переменное обозначено одной и той же буквой х), как, например, у = ax + b и у = (х—b)/a, у = е^х и у =  ln х, симметричны по отношению к биссектрисе у = х первого и третьего координатных углов. Функция, обратная по отношению к однозначной функии, может быть многозначной (ср., например, функции х² и

). Для однозначности О. ф. необходимо и достаточно, чтобы данная функция у = f (x) принимала различные значения для различных значений аргумента. Для непрерывной функции последнее условие может выполняться только в том случае, если данная функция монотонна (имеются в виду функции действительного аргумента, принимающие действительные значения). О. ф. по отношению к непрерывной и монотонной функции однозначна, непрерывна и монотонна.