Решение задач с помощью рулетки
Сколько удовольствия может доставить геометрия на практике — возле дома, в поле, у реки! Линии, на концах которых оказываются не буквы, а вешки, оживают, становятся осязаемыми С помощью рулетки, вешек и простейших самодельных приборов можно решать разные геометрические задачи: восстанавливать перпендикуляры, узнавать ширину реки и, наконец, заняться съемкой плана пионерлагеря.
Дальше в книжке будет говориться о геометрии на практике. Я разберу с вами несколько задач[9].
Эти задачи интересно решать в поле, а не читать о них, сидя за столом.
Организуйте в вашей школе или в пионерском лагере топографический кружок. Предположим, что желающих заниматься топографией оказалось 35 человек.
Разбейтесь на звенья по 3-6 человек. Выберите старших — звеньевых, которые распределят между остальными ребятами определенные обязанности. Пусть один будет идти впереди с вешками (вешильщик), двое будут измерять расстояния рулеткой, Двое — ковыльком (мерщики), один или двое будут записывать и рисовать, один будет заколачивать колышки, один собирать вешки и т. д. И эти свои обязанности ребята пусть не меняют.
Звенья могут заниматься на разных участках, а могут, наоборот, и на одном и том же участке. Тогда, по окончании занятий, можно будет сравнивать, у какого звена получились лучшие результаты.
Разбивка волейбольной площадки. В пионерском лагере понадобилось разбить волейбольную площадку размером 18 X 9 метров. Можно, конечно, сделать это на глазок, а можно и более точно, с помощью рулетки.
Помните теорему Пифагора — сумма квадратов катетов равна квадрату гипотенузы? Есть такой прямоугольный треугольник, у которого катеты равны 3 и 4 единицам, а гипотенуза — 5. Этот треугольник называется египетским, потому что соотношение его сторон было известно еще в древнем Египте.
Отмерим сперва линию АВ — 18 метров и отметим на ней на расстоянии 3 метров от А точку Е. В точках А, В, Е забьем колышки. Пусть один из вас держит ноль рулетки у колышка А, другой возьмет ленту за 9-й метр и приставит ее к точке Е, а третий возьмет ленту за 4-й метр, согнет ее и оттянет в сторону АС; лента неизбежно попадет своим 4-м метром в точку F. Забив в точке F колышек, нетрудно убедиться, что угол FАЕ будет прямым.
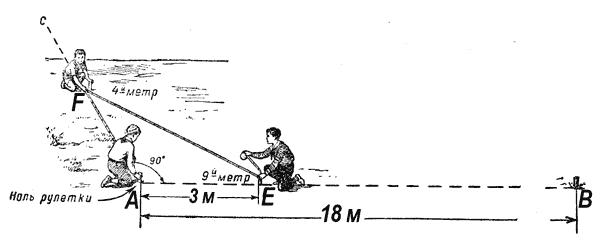
Ясно, чтобы получить точку С, надо продолжить рулеткой линию АF еще на 5 метров и поставить колышек С в створе колышков А и F.
Точно так же восстановим другой перпендикуляр, из точки В, и получим точку D.
Три стороны у нас измерены. Четвертую — СD — для контроля тоже необходимо измерить. Также необходимо измерить обе диагонали: АD и ВС (которые в прямоугольнике должны быть равны).
Если все эти контрольные измерения дадут ошибку менее 10 сантиметров, можно, переставляя немного колышки, добиться того, что разбивка волейбольной площадки по всем размерам — и основным и контрольным — будет вполне удовлетворительна.
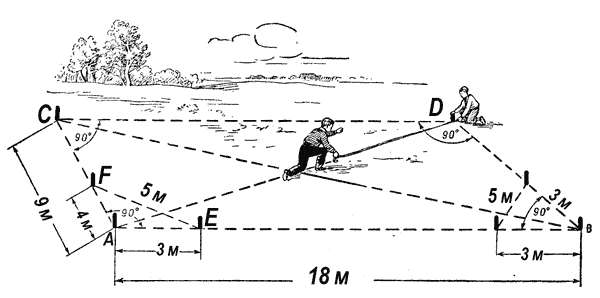
Если у вас рулетка 20-метровая, берите стороны треугольника соответственно вдвое больше: 10, 8 и 6 метров.
Опускание перпендикуляра. В том же пионерском лагере понадобилось при разбивке цветников опустить перпендикуляр из определенной точки С на линию АВ.
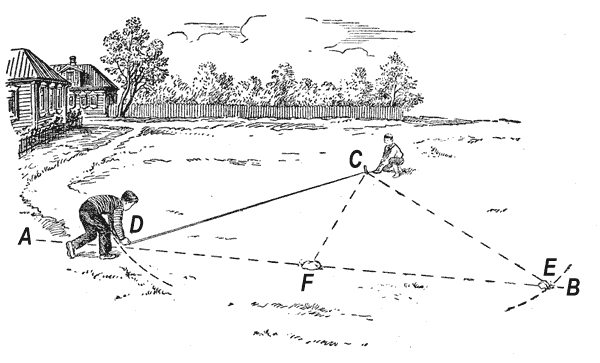
Пусть один из вас держит конец рулетки в точке С, а другой возьмется за коробку рулетки, развернет ленту и проведет ею дугу, как бы огромным циркулем. Эта дуга пересечет линию АВ в двух точках: 0 и Е. Разделите линию DЕ пополам и получите линию СF, перпендикулярную АВ (потому что линия СF соединяет середину хорды DЕ с центром круга — точкой С).
Проведение параллельной линии. В пионерском лагере может встретиться и такая задача: параллельно дорожке АВ надо провести другую дорожку, проходящую через точку С.
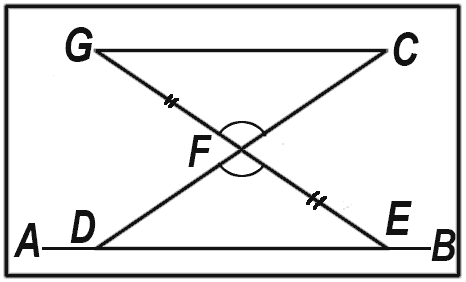
Выберите на дорожке АВ какие-нибудь точки D и Е, измерьте линию СD и в середине ее поставьте вешку F, затем измерьте линию ЕF, провешите ее дальше и на этом продолжении отложите отрезок FG, равный ЕF. Получилось два равных треугольника (так как две стороны и угол между ними равны). Значит, ∠ Е = ∠ С и ∠ D = ∠ С, а если так, то линии АВ и СG параллельны.
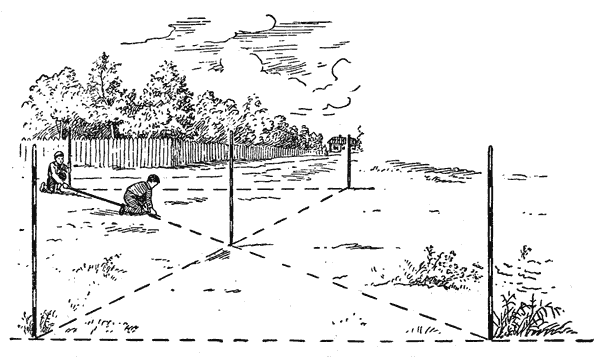
В задачах с одной рулеткой вы, очевидно, чувствуете некоторую громоздкость всех построений, особенно в случае параллельных линий, а перпендикуляры с помощью рулетки можно восстанавливать и опускать только короткие; 9-метровые перпендикуляры при разбивке волейбольной площадки уже чересчур длинны. Для построения коротких перпендикуляров топографы очень часто употребляют способ египетского треугольника. Ну, а как же быть, если вам понадобится разбить настоящее футбольное поле?