Ошибки большие и маленькие
Все это я вам рассказал о нивелировке технической и описал так называемый нивелир с уровнем при подставке. Но теперь такие инструменты больше не выпускаются: их постепенно вытесняют нивелиры глухие, в которых уровень спрятан глубоко в специальном кожухе и наглухо соединен с трубой.
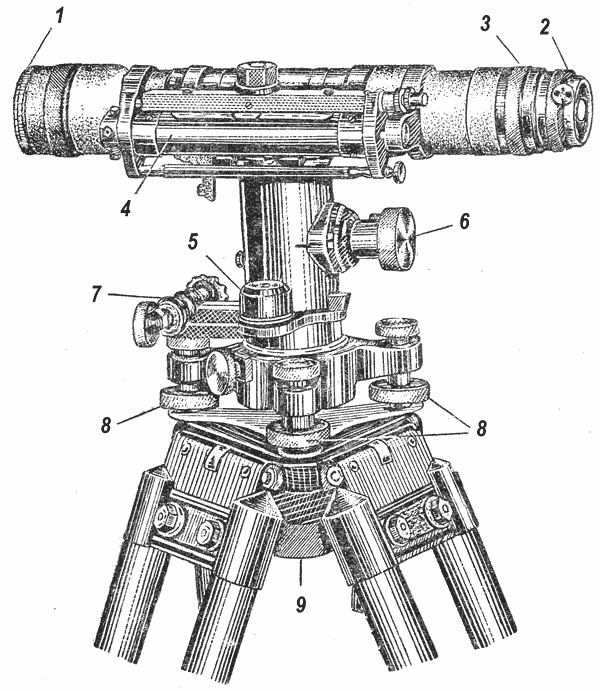
Поверять такие нивелиры несколько сложнее, но раз все части у него закрыты и жестко соединены между собой, эти поверки можно производить довольно редко. Зато устанавливать такие нивелиры гораздо проще и быстрее. У них благодаря системе призм и зеркал пузырек уровня виден в специальное отверстие возле окуляра, и вы можете одновременно правым глазом глядеть на рейку в трубу, а левым следить за пузырьком, при этом слегка подкручивая один из подъемных винтов, и когда пузырек будет медленно проползать через середину уровня, нужно моментально брать отсчет.
При обычном нивелировании можно ошибиться на 2-3 миллиметра на каждой стоянке инструмента, только надо устанавливать инструмент примерно посередине между пикетами. Ошибки эти неизбежны, но их нечего бояться. Практически эта неточность на толщину спички на расстоянии 100 метров не играет никакой роли, но самое главное — эти ошибки идут и в ту и в другую сторону и поэтому покрывают друг друга. Сумма ошибок (невязка) на 10 километров нивелирного хода обычно редко бывает больше 20 миллиметров.
Помню, когда я только начинал работать, я принес невязку в 4 миллиметра на 3 километра хода и был на седьмом небе от радости и гордости, считая такую невязку замечательным достижением техники, а оказалось, что это самая обычная невязка, которую разбрасывают по всем пикетам.
В математике существует теория ошибок, в которой такие покрывающие друг друга ошибки называются случайными.
Гораздо опаснее ошибки систематические, которые могут быть меньше случайных, но идут все время с одним знаком и постепенно накапливаются. Характерный пример систематической ошибки — измерение линий неправильной лентой.
Систематические ошибки зависят часто от недостатков самого инструмента. Ошибки случайные зависят от многих причин: пузырек уровня сошел немного в сторону; точка-колышек в земле шатается; реечник наклонил рейку; неточно оценивались на глаз миллиметры на рейке; наконец, труба на какую-то долю микрона не горизонтальна.
Большое искушение шагать с нивелиром через пикет, то-есть через 200 метров — цифры и шашки на рейке в трубу ведь хорошо видны, — но с увеличением расстояния случайные ошибки увеличиваются.
Грубые ошибки, если их не заметишь, могут привести к неприятным последствиям. А при нивелировании ошибиться сразу и намного очень легко (5 сантиметров — это уже много).
Вот пример. Собирается дождик; хочется закончить работу поскорее: поспешил, посмотрел чересчур быстро в трубу; показалось, что на рейке 29 дециметров, а на самом деле нить «била» на 19, вот и ошибка на 10 дециметров — на целый метр.
Может быть и так. В день полагается проходить до 8 километров, приходится делать множество записей четырехзначных цифр; работа однообразная; посмотрел на заднюю рейку, на секунду внимание ослабло, и цифру записал в графе «передние взгляды». Выходит, опять ошибся.
А бывает, виноват и реечник. Ему кричат: «Станови скорее!» Реечник туда, сюда — нет точки, пропала, — и поставил рейку на сторожок. Техник спокойно навел трубу, записал цифру и перенес инструмент на другое место. А пока он его устанавливал, реечник нашел точку и, ничего не сказав, поставил на нее рейку. Техник вновь посмотрел в трубу, уже задним взглядом, записал новую цифру и пошел дальше. Он и не подозревал, что рейка была переставлена. А ведь непрерывная цепь взглядов оборвалась, и получилась ошибка на высоту сторожка.
Ошибки нивелировщика могут привести к тяжелым последствиям. Например, выкопали канал, а вода по нему не потекла. Почему? Оказывается, где-то нивелировщик неверно записал цифру и во-время этого не заметил.
Гарин-Михайловский в своей книге «Инженеры» упоминает, как один нивелировщик на строительстве железной дороги ошибся на целую сажень, то-есть на 2,13 метра, и это заметили, когда сомкнули два соседних участка. Поезд на такую ступеньку ведь не прыгнет.
Раз так легко напутать, полагается каждый ход проверять два раза — туда и обратно — или, еще лучше, поручать каждую работу двум нивелировщикам с двумя разными инструментами. Если ход — замкнутый круг, полагается возвращаться к той точке, откуда была начата работа. Понятно, что тогда сумма всех превышений, положительных и отрицательных, теоретически должна быть равна нулю.
Значит, контроль дважды, даже трижды контроль, контроль везде, контроль постоянный и при нивелировке, да и вообще при геодезии совершенно обязателен. Без контрольных измерений топографы и геодезисты не имеют права работать. Вот почему так важно четко и аккуратно вести все записи в журнале.
«Людям свойственно ошибаться» — такова древнеримская, весьма пессимистическая поговорка. К топографам и геодезистам эти слова никак не подходят.
А если все-таки топограф ошибется?
Существует старинная русская пословица: «Семь раз отмерь, один раз отрежь». Вот эта пословица и является основным правилом геодезистов и топографов.
Разбивается здание. Кажется, что тут трудного — отмерили рулеткой 10 метров, и всё. Где тут можно ошибиться? А от того ли колышка вы отмерили? А в ту ли сторону вы направили рулетку? А когда начнут строить дом и увидят, что он поставлен наискось, что тогда делать?
Отмерьте свои 10 метров, а от полученной точки отмерьте контрольное расстояние до другой точки, да постарайтесь привязаться еще к третьей, да как-нибудь наискосок, да проверьте диагонали прямоугольника, да высчитайте по теореме Пифагора, какой должна быть их длина теоретически.
Благодаря контролю грубая ошибка всегда будет найдена и исправлена.
Какие огромные убытки могла бы принести ошибка геодезиста, скажем, если бы штольни при строительстве метро не встретились друг с другом, а прошли мимо!
Сперва спускается в шахту один геодезист со своими инструментами, производит необходимые, подчас очень сложные, измерения; потом спускается другой, также со своими инструментами, и проделывает ту же работу; потом они передают свои журналы двум вычислителям, а третий проверяет вычисления. Тут уже будет полная гарантия, что ошибок нет и штольни сойдутся во всех трех измерениях с точностью до сантиметра.
Когда геодезист ведет съемку, он обязательно замыкает все свои хода обоснования и по координатам вычисляет невязку. Если невязка получится недопустимая, он не успокаивается до тех пор, пока не найдет ошибку. Сперва он ищет ее в вычислениях: при четырех действиях арифметики ошибиться гораздо легче, чем при полевых измерениях. Если же он ошибку не найдет, значит надо искать ее в поле.
В замкнутом полигоне углы увязались, а линии не увязались — значит, ошибка скрывается в одной из линий. Чаще всего так оно и бывает. Случаются ошибки и грубые.
Если грубая ошибка одна — скажем, в одной линии не хватает 20 метров, — найти ее, как правило, очень легко. Но если грубых ошибок несколько — например, линии измерены правильно, а в одном углу геодезист сперва ошибся на 1° в одну сторону, а в другом углу — на 1° в противоположную сторону, — линии и показали что-то не то. Такую ошибку отыскать трудно: геодезист будет по три раза перемерять все линии и не скоро догадается искать ее в углах.
Интересный случай произошел на практике с двумя студентами — Костей М. и Шурой С. Им было дано задание: выяснить, где легче провести оросительный канал — по левому или правому пути.
Для этого они должны были пронивелировать оба направления. Расстояние до конечной точки равнялось 5 километрам.
Первым в начальный пункт приехал со своими рабочими Костя. Это была крайняя улица города. Он увидел деревянный дом на кирпичном фундаменте:
— Вот отсюда и начну.
И Костя поставил рабочего с задней рейкой на угол цоколя фундамента этого дома. Переднюю рейку он послал на пикет по пути будущего канала.
Шура что-то запаздывал, и Костя прикрепил на сторожке первого пикета записку:
«Шура, я начал с крайнего по ходу угла цоколя дома А. Дружинниковой. К.».
Оставив записку, Костя отправился с нивелиром по своему пути. Через десять минут приехал Шура, увидел записку, оглянулся по сторонам, и на одном из домов ему попалась на глаза дощечка: «Дружинникова».
— Ага, Дружинникова! Крайний угол цоколя фундамента. Что же он, хотя бы карандашом на кирпиче крестик поставил... Ну ладно, — обратился Шура к рабочему, — ставь рейку на самый угол.
К вечеру оба студента встретились в конечном пункте на дне оврага, приехали вместе домой, поужинали и засели считать превышения.
Цоколь дома Дружинниковой был выше дна оврага на определенное число метров, каким путем ни иди. А у студентов получилось так: у Шуры оказалось 8,325 метра, у Кости — 10,711 метра. Прикинули вновь на счетах. Нет, не видно, где напутали. Стало быть, ошибка произошла в поле, и большая ошибка — больше 2 метров. Кто же был виноват? Втайне каждый надеялся, что не он.
Пришлось на следующий день начинать работу сызнова. И на этот раз Костя со своими рабочими приехал раньше.
Вечером стали считать, и опять оказалась ошибка на 2,379 метра. Что за штука! Накануне ошиблись только на 7 миллиметров больше! Сравнили отдельные превышения между пикетами. Они примерно сходились, но возле города получалось что-то не то.
— Ага, нашли, по крайней мере, место ошибки!