Коротко можно сказать, что Э. г. включает те вопросы геометрии, которые в своей постановке и решении не включают общей концепции бесконечного множества, но лишь конструктивно определённые множества (геометрические места). Когда говорят, что евклидова геометрия основана, скажем, на системе аксиом Гильберта или на иной, близкой по характеру системе аксиом то забывают что при введении общих понятий кривой выпуклого тела длины и др. фактически используют способы образования понятий, вовсе не предусмотренные в аксиомах, а опирающиеся на общую концепцию множества, последовательности и предела, отображения или функций. То, что выводится из аксиом Гильберта без таких добавлений, и составляет элементарную часть евклидовой геометрии. Это разграничение можно уточнить в терминах математической логики. Вместе с тем, соответственно такому пониманию Э. г., можно говорить об Э. г. n -мерного евклидова пространства, о Э. г. Лобачевского и др. При этом имеются в виду те разделы, теоремы и выводы этих геометрических теорий, которые характеризуются теми же чертами.

  Лит.: Начала Евклида, пер. с греч., кн. 1—15, М. — Л., 1948—50; Адамар Ж., Элементарная геометрия пер. с фр., ч. 1, 4 изд., М., 1958; Погорелов А. В., Элементарная геометрия, 2 изд., М., 1974; История математики с древнейших времен до начала XIX столетия, т. 1—3, М., 1970—72.

Элементарная длина

Элемента'рная длина', то же, что фундаментальная длина .

Элементарная математика

Элемента'рная матема'тика, несколько неопределённое понятие, охватывающее совокупность таких разделов, задач и методов математики, в которых пользуются общими понятиями переменной функции предела и т п. Иначе говоря Э. м. пользуется теми общими понятиями (абстракциями), которые сложились до появления математического анализа; хотя Э. м. продолжает развиваться и теперь и в ней появляются новые результаты, всё же это происходит в рамках тех же понятий (см. ст. Математика раздел II. История математики до 19 в., пункт 2 — Период элементарной математики).

  Э. м. охватывает в основном арифметику и т. н. элементарную теорию чисел, элементарную алгебру, элементарную геометрию, тригонометрию. Коротко Э. м. можно характеризовать как «математику постоянных величин» Это однако не совсем точно, т. к. в Э. м. рассматривают не только постоянные величины, но и геометрические фигуры (не обязательно интересуясь их величиной, например расположением), и не только постоянные, но и переменные величины, например тригонометрические функции. Здесь речь идет о некоторых (конкретно определенных) функциях. Точно также, например, при определении длины окружности пользуются по существу понятием предела, но не в общем виде, а лишь для конкретно определенной последовательности (периметров вписанных и описанных многоугольников). Общие же понятия функции и предела, так же как и общие понятия кривой, поверхности, фигуры вообще не заданной каким-либо конкретным построением, заведомо выходят за пределы Э. м. Например, в теории чисел отличают элементарные доказательства, в которых обходятся без методов математического анализа. Кстати, эта «элементарная теория чисел» вовсе не является элементарной в смысле простоты

  Э. м. в противоположность высшей математике понимают ещё просто как совокупность математических дисциплин, изучаемых в средней общеобразовательной школе.

Элементарная нить

Элемента'рная нить, одиночная нить, не делящаяся в продольном направлении без разрушения. Является составной частью текстильных комплексных нитей. К Э. м. относятся химические нити различного вида, а также шелковина (одна из двух нитей, составляющих коконную нить). См. также Волокна текстильные .

Элементарная операция

Элемента'рная опера'ция, микрооперация, в вычислительной технике, элементарное машинное действие, не содержащее др. более простых действий, обозначенных в языке ЦВМ. Реализация каждой команды ЦВМ состоит из последовательного выполнения некоторого количества операций , в том числе таких Э. о., как установка регистра в нулевое положение, запись нуля в ячейки памяти, сдвиг влево или вправо на 1 разряд кода в регистре, передача информации между регистрами и др., а также сравнение кодов, логическое сложение и умножение и т. д. Набор Э. о. должен обеспечивать алгоритм выполнения любой системы команд ЦВМ. Э. о. могут объединяться в группы, на основе которых организуется микропрограммное управление ЦВМ.

Элементарная теория музыки

Элемента'рная тео'рия му'зыки, первоначальный учебный музыкально-теоретический курс, преподаваемый в музыкальных школах и включающий нотную грамоту, основные сведения о важнейших элементах музыки, средствах музыкальной выразительности (музыкальные звуки, интервалы, аккорды, лад, метр, ритм, темп, динамика и др.).

  Лит.: Способин И, В., Элементарная теория музыки. М., 1954.

Элементарная ячейка

Элемента'рная яче'йка кристалла, минимальный объём кристалла, параллельные переносы (трансляции) которого в трёх измерениях позволяют построить всю кристаллическую решётку. Выбор Э. я. может быть произведён различными способами.

Элементарное волокно

Элемента'рное волокно', одиночное волокно текстильное , не делящееся в продольном направлении без разрушения и пригодное для изготовления пряжи и текстильных изделий.

Элементарные делители

Элемента'рные дели'тели квадратной матрицы А = ||a_iK ||₁ ⁿ , степени двучленов

(l — l₁ ) _{p 1} , (l — l₂ ) _{p 2} ,..., (l — l_s ) _ps ,

которые получаются из характеристического уравнения

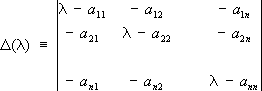
следующим образом. Миноры k-го порядка определителя D(l) (для k £ п ) представляют собой многочлены относительно l. Пусть D_k (l) (k = 1, 2,..., n ) - наибольший общий делитель всех этих многочленов, D_n (l) = D(l). В ряду каждый многочлен делится на предыдущий без остатка. Если разложить соответствующие частные на линейные множители в поле комплексных чисел:

.............................……………………………..,

то степени

,...,

,... и образуют полную систему Э. д. матрицы А (при этом степени с нулевыми показателями не принимаются во внимание). Произведение всех Э. д. равно характеристическому многочлену. Э. д. определяют нормальную (жорданову) форму матрицы А.