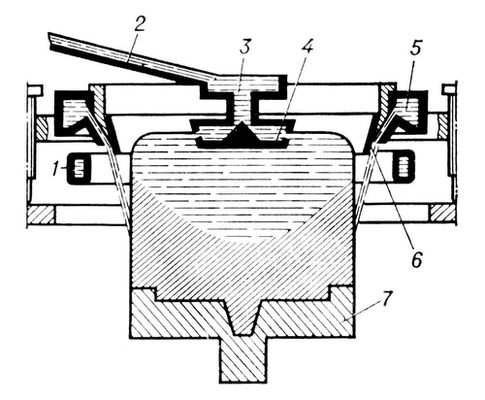
Рис. 1. Схема непрерывного литья в электромагнитный кристаллизатор: 1 — индуктор; 2 — лоток; 3 — распределительная коробка; 4 — плавающая чаша; 5 — коллектор; 6 — направляющий конус; 7 — поддон.

Непрерывное производство

Непреры'вное произво'дство, совокупность непрерывных технологических процессов, организованных в виде производственной линии, участка, цеха или предприятия в целом. Характерно для отраслей промышленности, производящих однородную основную продукцию (металлургия и др.), осуществляющих массовый выпуск продукции, состоящих из отдельных комплектующихся в единое целое частей (автомобилестроение, тракторостроение, швейная промышленность и др.), для отраслей промышленности, непрерывность производства в которых диктуется характером технологии (выработка электроэнергии, производство химических и пищевых продуктов). Н. п., как правило, сокращает время производства продукции, способствует росту производительности труда, обеспечивает более полное использование основных фондов и ускорение оборачиваемости оборотных средств. Наибольшего эффекта оно достигает в условиях поточного производства . С ускорением научно-технического прогресса сфера Н. п. значительно расширяется в результате механизации и автоматизации не только основных, но и вспомогательных производств.

Непрерывности аксиомы

Непреры'вности аксио'мы, аксиомы, выражающие тем или иным образом непрерывность прямой линии. Например, аксиома Дедекинда: если все точки прямой разбиты на два непустых класса, причём все точки первого класса расположены левее всех точек второго, то существует либо самая правая точка первого класса, либо самая левая точка второго; аксиома Кантора: любая последовательность вложенных друг в друга отрезков, длины которых стремятся к нулю, имеет одну общую точку. Н. а. дают возможность устанавливать сохраняющее порядок взаимно однозначное соответствие между совокупностью всех точек прямой и совокупностью всех действительных чисел. Д. Гильберт предложил в качестве Н. а. Архимеда аксиому и аксиому о невозможности присоединения к прямой новых точек с сохранением аксиом упорядоченности, конгруэнтности и аксиомы Архимеда (аксиома линейной полноты).

Непрерывность

Непреры'вность, одно из важнейших математических понятий, встречающееся в двух основных концепциях — Н. множества и Н. отображения. Исторически раньше подверглось математической обработке понятие непрерывного отображения, или непрерывной функции , чем логически предшествующее ему понятие «Н. множества». Понятие непрерывной действительной функции обобщается на произвольные отображения так: однозначное отображение у = f (x ) некоторого множества Х элементов х на множество Y элементов у называется непрерывным, если из сходимости последовательности x₁ , x₂ ,..., x_n ,... элементов множества Х к элементу х следует сходимость их образов f (x₁ ), f (x₂ ),.. ., f (x_n ), ... к образу f (x ) предельного элемента х (о других обобщениях того же понятия см. в ст. Топология ). Т. о., определение Н. отображения зависит от того, как в самих множествах Х и Y определены предельные соотношения (в нашем случае сходимость последовательностей). Множество элементов с определёнными предельными соотношениями между ними называется в современной математике топологическим пространством . В терминах теории топологических пространств в настоящее время обычно и излагаются понятия, характеризующие свойства Н. различных множеств математических объектов. Об этих понятиях см. в ст. Континуум .

  Лит.: Дедекинд Р., Непрерывность и иррациональные числа, пер. с нем., 4 изд., Одесса, 1923; Кантор Г., Основы общего учения о многообразиях, [пер. с нем.], в кн.: Теория ассамблей. 1, СПБ, 1914 (Новые идеи в математике, сб. 6); Гильберт Д., Основания геометрии, пер. с нем., М. — Л., 1948; Хаусдорф Ф., Теория множеств, пер. с нем., М. — Л., 1937; Александров П. С., Введение в общую теорию множеств и функций, М. — Л., 1948.

Непрерывность судебного разбирательства

Непреры'вность суде'бного разбира'тельства, см. в ст. Непосредственность , непрерывность и устность судебного разбирательства .

Непрерывный спектр

Непреры'вный спе'ктр, то же, что сплошной спектр .

Непрерывный стаж работы

Непреры'вный стаж рабо'ты, см. в ст. Стаж трудовой .

Неприводимое уравнение

Неприводи'мое уравне'ние, алгебраическое уравнение f (x ) = 0, левая часть которого не разлагается на множители, т. е. представляет собой неприводимый многочлен . Если уравнение не является неприводимым, то решение его облегчается тем, что оно сводится к решению нескольких алгебраических уравнений более низкой степени.

Неприводимый многочлен

Неприводи'мый многочле'н , многочлен, не разлагающийся на множители более низкой степени. Возможность разложить многочлен на множители (и свойство неприводимости) зависит от того, какие числа допускаются в качестве коэффициентов многочлена. Так, многочлен x³ + 2 неприводим, если в качестве коэффициентов допускать только рациональные числа, но разлагается в произведение двух Н. м.

если в качестве коэффициентов брать любые действительные числа, и в произведение трёх множителей

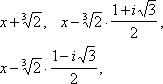
если коэффициентами будут числа комплексные. В общем случае понятие неприводимости определяется для многочленов с коэффициентами, принадлежащими произвольному полю (см. Поле алгебраическое). Часто Н. м. называют многочлен с рациональными коэффициентами, не разлагающийся на множители более низкой степени также с рациональными коэффициентами.

  Лит.: Курош А. Г., Курс высшей алгебры, 9 изд., М., 1968.