УНРС радиального и криволинейного типов, у которых неполностью затвердевшая заготовка выходит на горизонтальный участок, позволяют значительно повысить скорость разливки при крупных сечениях заготовки, так как участок резки может быть расположен на достаточно большом расстоянии от кристаллизатора (30—35 м ). Общая высота таких установок, как правило, не превышает 12 м.

  На УНРС отливаются заготовки квадратного сечения размером от 50x50 до 300x300 мм, плоские слябы толщиной от 50 до 300 мм и шириной от 300 до 2000 мм, круглые заготовки (сплошные и с внутренней полостью) диаметром от 100 до 550 мм, из которых получают трубы, сортовой и листовой прокат, поковки. Большая степень химической однородности по длине и поперечному сечению непрерывнолитых заготовок обеспечивает стабильные механические свойства и повышает надёжность работы металлоизделий. Благодаря своим преимуществам Н. р. с. принята в качестве основного способа разливки во всех вновь сооружаемых сталеплавильных цехах и будет широко использоваться при реконструкции действующих заводов. Наибольшая производительность УНРС обеспечивается при их работе в сочетании с кислородными конвертерами. В этом случае достигается равенство циклов выпуска стали из конвертера и разливки её на УНРС, благодаря чему жидкий металл может подаваться на установку непрерывно в течение длительного времени. В цехах с современными дуговыми печами, продолжительность плавки в которых выдерживается достаточно точно, также может быть организована разливка так называемым методом «плавка на плавку» (одна установка непрерывно принимает металл от нескольких печей). Перспективны агрегаты, в которых Н. р. с. совмещается с непрерывной прокаткой в едином потоке. При этом снижаются затраты энергии, повышаются качество слитка и выход годного, сокращается цикл производственных операций от выплавки стали до получения готового проката. Такие агрегаты уже вступили в эксплуатацию, как в СССР, так и за рубежом. В соответствии с прогнозом развития чёрной металлургии, к 1990 в СССР непрерывным способом будет разливаться около 60% всей выплавляемой стали; при этом мощностей по её производству потребуется на 30 млн. т меньше, чем при обычной разливке.

  Лит.: Бойченко М. С., Рутес В. С., Фульмахт В. В., Непрерывная разливка стали, М., 1961; Шварцмайер В., Непрерывная разливка, пер. с нем., М., 1962; Германн Э., Непрерывное литье, пер. с нем., М., 1961; Теория непрерывной разливки. Технологические основы, М., 1971.

  Д. П. Ефтеев.

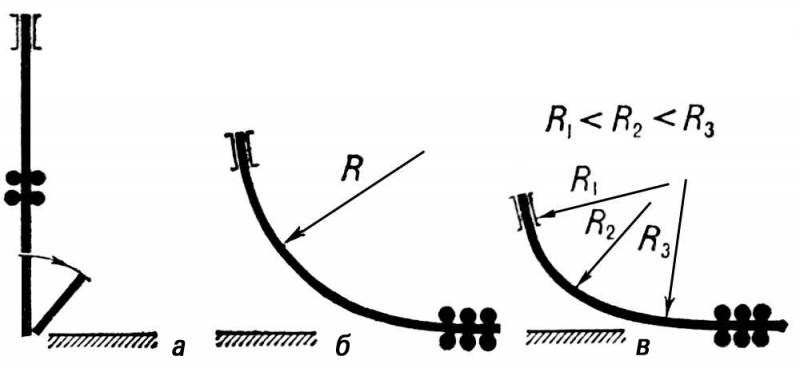
Рис. 2. Схемы УНРС вертикального (а), радиального (б) и криволинейного (в) типов.

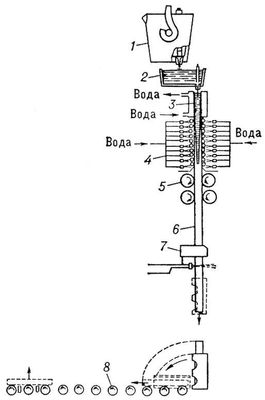
Рис. 1. Принципиальная схема УНРС: 1 — сталеразливочный ковш; 2 — промежуточный ковш (предназначен для снижения и стабилизации напора металла, поступающего в кристаллизатор, и для распределения металла по нескольким кристаллизаторам на многоручьевых установках); 3 — кристаллизатор; 4 — зона вторичного охлаждения с устройствами для направления заготовки и подачи воды; 5 — тянущие валки; 6 — слиток; 7 — устройство для разрезки заготовки (кислородные резаки или ножницы); 8 — устройство для выдачи заготовки.

Непрерывная функция

Непреры'вная фу'нкция, функция , получающая бесконечно малые приращения при бесконечно малых приращениях аргумента. Однозначная функция f (x ) называется непрерывной при значении аргумента x , если для всех значений аргумента х, отличающихся достаточно мало от x , значения функции f (x ) отличаются сколь угодно мало от её значения f (x ). Точнее, функция f (х ) называется непрерывной при значении аргумента x (или, как говорят, в точке x ), если каково бы ни было e > 0, можно указать такое d > 0, что при |х — х | < d будет выполняться неравенство |f (x ) — f (x )| < e. Это определение равносильно следующему: функция f (x ) непрерывна в точке x , если при х, стремящемся к x , значение функции f (x ) стремится к пределу f (x ). Если все условия, указанные в определении Н. ф., выполняются только при х ³ х или только при х £ х , то функция называется, соответственно, непрерывной справа или слева в точке x . Функция f (x ) называется непрерывной н а отрезке [а , b ], если она непрерывна в каждой точке х при а < х < b и, кроме того, в точке а непрерывна справа, а в точке b — слева.

  Понятию Н. ф. противопоставляется понятие разрывной функции . Одна и та же функция может быть непрерывной для одних и разрывной для других значений аргумента. Так, дробная часть числа х [её принято обозначать через (х )], например

является функцией разрывной при любом целом значении и непрерывной при всех других значениях (рис. 1 ), причём в целочисленных точках она непрерывна справа.

  Простейшими функциями переменного х, непрерывными при всяком значении x , являются многочлены, синус (у = sin x), косинус (у = cos x), показательная функция (у = a^x , где а — положительное число). Сумма, разность и произведение Н. ф. снова дают Н. ф. Частное двух Н. ф. также есть Н. ф., за исключением тех значений х, для которых знаменатель обращается в нуль (так как в таких точках рассматриваемое частное не определено). Например,

есть Н. ф. для всех значений х, кроме нечётных кратных p/2, при которых cosх обращается в нуль.

  Н. ф. обладают многими важными свойствами, которыми и объясняется огромное значение этих функций в математике и её приложениях. Одно из важнейших свойств выражается следующей теоремой: для всякой функции, непрерывной на отрезке [а, b ] можно найти многочлен, значения которого отличаются на этом отрезке от значений функции менее чем на произвольно малое, наперёд заданное число (теорема о приближении Н. ф. многочленами). Справедлива также и обратная теорема: всякая функция, которую на некотором отрезке можно с произвольной степенью точности заменить многочленом, непрерывна на этом отрезке.

  Функция, непрерывная на отрезке, ограничена на нём и достигает на этом отрезке наибольшего и наименьшего значения (см. Наибольшее и наименьшее значения функций ). Кроме того, она принимает на этом отрезке все значения, лежащие между её наименьшим и наибольшим значениями. Функции, непрерывные на отрезке, обладают свойством равномерной непрерывности . Всякая функция, непрерывная на некотором отрезке, интегрируема на нём, т. е. является производной другой Н. ф. Однако не всякая Н. ф. сама имеет производную. Геометрически это означает, что график Н. ф. не обязательно обладает в каждой точке определённым направлением (касательной); это может произойти, например, потому, что график имеет угловую точку (рис.2 , функция у = |x |), или потому, что он совершает в любой близости точки О бесконечно много колебаний между двумя пересекающимися прямыми (рис. 3 , функция