В реальных средах нередко скорости распространения синусоидальных В. зависят от частоты В. (так называемая дисперсия волн). Поэтому негармоническая В. (т. е. совокупность гармонических В. различных частот) в процессе распространения меняет свою форму вследствие того, что при распространении этих гармонических В. соотношение между их фазами меняется. Искажение формы В. может происходить и при дифракции и рассеянии негармонических В., так как оба эти процесса зависят от длины В. и поэтому для гармонической В. разной длины дифракция и рассеяние будут происходить по-разному. При наличии дисперсии изменение формы негармонической В. может происходить также в результате преломления В. Однако иногда может искажаться и форма гармонической В. Это происходит в тех случаях, когда амплитуда распространяющейся В. достаточно велика, так что уже нельзя пренебрегать изменениями свойств среды под воздействием В., т. е. когда сказываются нелинейные свойства среды. Искажения формы синусоидальной В. могут выразиться в том, что «горбы» В. (области больших возмущений) распространяются со скоростью, превышающей скорость распространения остальных участков В., в результате чего синусоидальная форма В. превращается в пилообразную (рис. 11 ). В нелинейной среде существенно изменяются и другие законы распространения В. — в частности, законы отражения и преломления. Подробнее см. Нелинейная оптика .

  Фазовая и групповая скорости В. Введённая выше скорость В. называется фазовой скоростью, это скорость, с которой перемещается какая-нибудь определённая фаза бесконечной синусоидальной В. (например, фаза, соответствующая гребню или впадине), фазовая скорость В. входит, в частности, в формулу закона преломления. Однако на опыте имеют дело с В. не в виде бесконечных синусоид, называемых также монохроматическими В., для которых только и имеет смысл понятие фазовой скорости, а с ограниченными В. Как уже было указано, любая ограниченная В. может быть представлена в виде наложения большого (точнее — бесконечно большого) числа монохроматических В. различных частот. Если фазовые скорости В. всех частот одинаковы, то с этой же скоростью распространяется и вся совокупность, или группа, В. Если же эти скорости не одинаковы, т. е. имеет место дисперсия, то вопрос о скорости распространения ограниченной. В. усложняется. Английским физиком Дж. У. Рэлеем было показано, что если ограниченная В. составляется из В., частоты которых мало отличаются друг от друга, то эта В., или как её часто называют волновой пакет, распространяется с определённой скоростью, называемой групповой скоростью. Групповая скорость u вычисляется по формуле: u = с - λdc/dλ . С групповой скоростью происходит также перенос энергии В.

  Изменение частоты В. при движении источника или наблюдателя (эффект Доплера). Наблюдатель, движущийся по направлению к источнику В. (любого вида), воспринимает несколько повышенную частоту по сравнению с неподвижным наблюдателем, между тем как наблюдатель, удаляющийся от источника В., воспринимает пониженную частоту. Аналогичное явление (качественно) имеет место также, когда наблюдатель неподвижен, а источник В. движется. Это явление называется Доплера эффектом .

  В. и лучи. Линия, направление которой в каждой точке совпадает с направлением потока энергии в В., называется лучом (рис. 9 , б). В изотропной среде это направление совпадает с направлением нормали к фронту В. Плоской В. соответствует параллельный пучок прямолинейных лучей, сферической В. — радиально расходящийся пучок и т.д. При некоторых условиях сложный расчёт распространения В. можно заменить более простым расчётом формы лучей. Этим пользуются в геометрической акустике и геометрической оптике . Такой упрощённый подход применим, когда длина В. достаточно мала по сравнению с некоторыми характерными размерами, например размерами препятствий, лежащих на пути распространения В., поперечными размерами фронта В., расстояний до точки, в которой сходятся В., и т.п.

  Излучение и распространение В. Для излучения В. необходимо произвести в среде некоторое возмущение за счёт внешнего источника энергии. Работа, совершаемая этим источником, за вычетом некоторых потерь превращается в энергию излучаемых В. Так, например, мембрана телефона или диафрагма громкоговорителя, получая энергию от электроакустического преобразователя , излучает звуковые В. Излучение В. производится всегда источниками ограниченных размеров, в результате чего возникает «расходящаяся» В. Только на достаточно большом расстоянии от источника эту В. можно принять за плоскую.

  Несмотря на разную природу В., закономерности, которыми определяется их распространение, имеют между собой много общего. Так, упругие В. в однородных жидкостях (газах) или электромагнитные В. в свободном пространстве (а в некоторых случаях и в пространстве, заполненном однородным изотропным диэлектриком), возникающие в какой-нибудь малой области («точке») и распространяющиеся без поглощения в окружающем пространстве, подчиняются одному и тому же волновому уравнению .

  Особого вида излучение В. имеет место при движении в среде тел со скоростями, большими, чем фазовые скорости В. в этой среде. Электрон, движущийся в какой-либо среде со скоростью, большей, чем фазовая скорость электромагнитных В., в этой среде излучает В. (Черенкова — Вавилова излучение ), при движении же со скоростью, меньшей фазовой скорости света в среде, это движение сопровождается лишь простым перемещением электрического и магнитного полей без перехода энергии движения в энергию излучения. Аналогично этому самолёт, движущийся со скоростью, большей скорости звука, излучает звуковую В. особого вида — ударную волну , и теряет на это определённую часть энергии. Излучением В. такого же происхождения, распространяющихся по поверхности воды, объясняется появление волнового сопротивления при движении корабля.

  Другие виды В. Известны также: а) температурные В., распространяющиеся в окрестности переменного во времени источника тепла; б) вязкие В. — поперечные (быстро затухающие) В. в вязкой жидкости; в) волны де Бройля , которыми в квантовой механике описывается поведение микрочастиц; г) гравитационные волны , излучаемые движущимися с ускорением массами.

  Лит.: Горелик Г. С., Колебания и волны, 2 изд., М., 1959; Красильников В. А., Звуковые и ультразвуковые волны в воздухе, воде и твердых телах, 3 изд., М., 1960; Бреховских Л. М., Волны в слоистых средах М., 1957.

  Л. М. Бреховских.

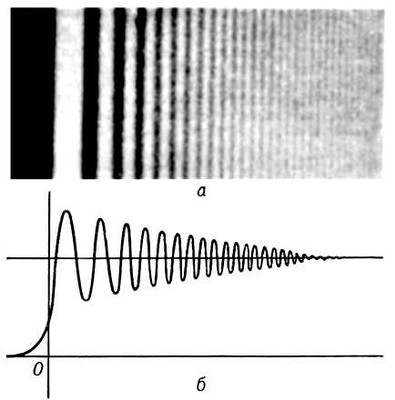
Рис. 7. а — дифракция света от края экрана; виден сложный переход от света к тени; б — кривая, характеризующая освещенность пространства между светом и тенью; край экрана в точке О.

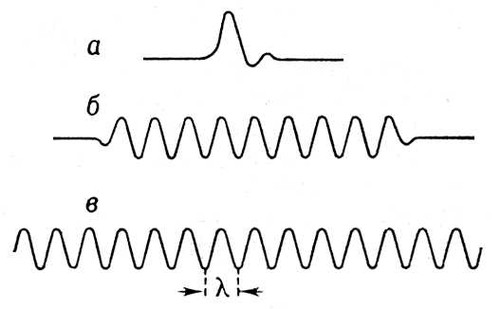
Рис. 2. а — одиночная волна; б — цуг волн; в — бесконечная синусоидальная волна.

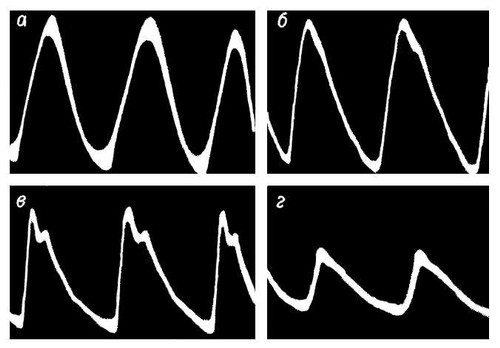
Рис. 11. Искажение формы синусоидальной волны большой интенсивности. На некотором расстоянии синусоидальная волна а превращается в пилообразную г (б и в — промежуточные стадии). Направление распространения волны справа налево.

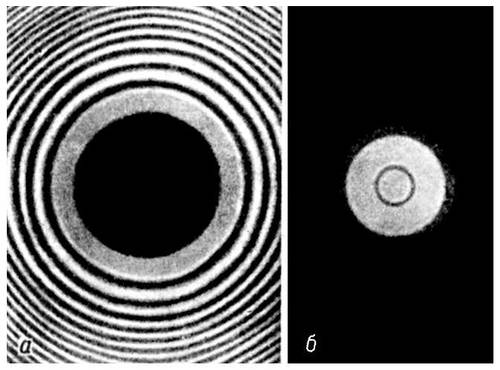
Рис. 6. Дифракционная картина при падении света: а — на круглый экран; б — на круглое отверстие.