М. К. Петров.

  Интерпретируя В. и д. как соотносительные понятия, выражающие основные моменты движения и развития бытия , диалектический материализм рассматривает возможность как менее богатое и конкретное понятие, чем действительность в широком смысле, т. е. объективный мир в целом с присущим ему различием, в том числе противоборствующими тенденциями. Марксизм указал на 2 взаимосвязанных момента: на внутреннее беспокойство, самодвижение, присущее бытию, которое по мере развития реализует свои собственные возможности, и на роль человеческой деятельности, общественной практики, которая имеет дело с определённым спектром возможностей (в том числе и создаваемых в самой человеческой истории) и превращает их в действительность. Действительность в узком смысле и есть реализация существующих потенций бытия и практики как его социальной формы. В этом смысле человеческая история — это история раскрытия объективных возможностей бытия, их реализация, создание новых объективных социально-культурных возможностей и их воплощение в практике.

  В зависимости от характера закономерностей, лежащих в основе того или иного типа возможностей, различают абстрактную и реальную возможности. Абстрактная возможность противостоит невозможности и вместе с тем не может непосредственно превратиться в действительность. Реальная возможность предполагает наличие объективных условий для её реализации. Различие между этими двумя типами возможности относительно, так как оба они основаны на объективных, хотя и разного порядка, закономерностях. При изменении условий абстрактная возможность может перерасти в реальную. Классический пример такого превращения дан К. Марксом при анализе генезиса кризисов: в условиях капитализма абстрактная возможность кризиса, возникающая из разделения процесса обмена на два акта — купли и продажи, становится реальной возможностью, которая превращается в действительность. Степень возможности того или иного явления выражается через категорию вероятности .

  В существовании и развитии любого объекта воплощено единство противоположных тенденций и потому содержатся возможности разного уровня, направления и значения. Конкретная совокупность реальных условий определяет, какая из возможностей становится господствующей и превращается в действительность; остальные же либо превращаются в абстрактную возможность, либо вообще исчезают. Различают объективные и субъективные условия превращения возможности в действительность. Последние специфичны для общества: здесь ни одна возможность не превращается в действительность, помимо деятельности людей. Вместе с тем субъективный момент деятельности открывает возможности для её волюнтаристского истолкования и соответствующих попыток реализации. Однако произвол в истории раньше или позже терпит крах именно в силу того, что он игнорирует реальные законы действительности, её реальные возможности. Марксизм подчёркивает решающую роль активности человека, его творческих усилий в реализации возможностей, в превращении осознанных тенденций общественного развития в действительность.

  Лит.: Маркс К., Тезисы о Фейербахе, Маркс К. и Энгельс Ф., Соч., 2 изд., т. 3; его же, Капитал, т. 1, там же, т. 23; Энгельс Ф., Диалектика природы, там же, т. 20; Ленин В. И., Крах II Интернационала, Полн. собр. соч.,5 изд., т. 26, с. 212— 219; его же, Философские тетради, там же, т. 29, с. 140—42, 321—22, 329—30; Гегель Г. В. Ф., Энциклопедия философских наук, Соч., т. 1, М. — Л., 1929; Проблема возможности и действительности, М.—Л., 1964; Арутюнов В. Х., О категориях возможности и действительности и их значении для современного естествознания, К., 1967.

  Л. Е. Серебряков.

Возможные перемещения

Возмо'жные перемеще'ния, виртуальные перемещения, элементарные (бесконечно малые) перемещения, которые точки механической системы могут совершать из занимаемого ими в данный момент времени положения, не нарушая наложенных на систему связей (см. Связи механические ). В. п. — понятия чисто геометрические, не зависящие от действующих сил; они определяются только видом наложенных на систему связей и вводятся как характеристики этих связей, показывающие, какие перемещения при наложенных связях остаются для системы возможными. Например, если связью для точки является какая-нибудь поверхность и точка находится на ней в данный момент в положении М (см. рис. ), то В. п. точки в этот момент будут элементарные отрезки (векторы) длиной d_s , направленные по касательной к поверхности в точке М. Перемещение по любому другому направлению не будет В. п., так как при этом нарушится связь (точка не останется на поверхности). Понятие В. п. относится и к покоящейся и к движущейся точке. Если связь со временем не изменяется, то истинное элементарное перемещение ds движущейся точки из положения М совпадает с одним из В. п.

  Понятием В. п. пользуются для определения условий равновесия и уравнений движения механической системы (см. Возможных перемещений принцип , Д’Аламбера — Лагранжа принцип ), а также при нахождении степеней свободы числа системы.

  С. М. Тарг.

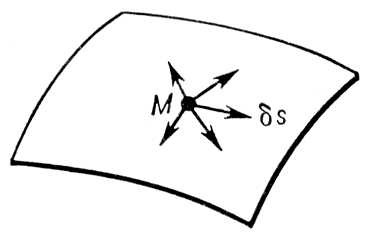
Рисунок к ст. Возможные перемещения.

Возможных перемещений принцип

Возмо'жных перемеще'ний при'нцип, один из вариационных принципов механики , устанавливающий общее условие равновесия механической системы. Согласно В. п. п., для равновесия механической системы с идеальными связями (см. Связи механические ) необходимо и достаточно, чтобы сумма работ dA_i , всех приложенных к системе активных сил на любом возможном перемещении системы была равна нулю. Математически В. п. п. выражается уравнением

 

где F_i — действующие активные силы, ds_i — величины возможных перемещений точек приложения этих сил, α_i — углы между направлениями сил и возможных перемещений. Для систем с несколькими степенями свободы уравнение (1) должно составляться для каждого независимого перемещения в отдельности.

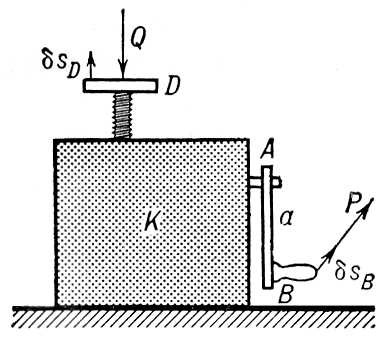
  Таким образом, В. п. п. позволяет найти условия равновесия системы, не вводя неизвестных реакций связей, что существенно упрощает решение и расширяет класс разрешимых задач. Например, с помощью В. п. п. легко найти условия равновесия подъёмного механизма, детали которого скрыты в коробке К (см. рис .). Из уравнения (1) получаем

 

где Р и Q — действующие силы. Для окончательного расчёта надо установить зависимость между перемещениями ds_B и ds_D . Если при одном повороте рукоятки АВ винт поднимается на величину h, то эта зависимость найдётся из пропорции ds_B : ds_D = 2pa : h , где а — длина рукоятки. Окончательно уравнение (2) даёт следующее условие равновесия Р = Qh/ 2pa . Методами геометрической статики (если скрытые в коробке детали механизма неизвестны) эта задача вообще решена быть не может.

  О применении аналогичного метода к решению задач динамики см. Д'Аламбера — Лагранжа принцип .

  С. М. Тарг.